Question 188391: At what time between 2 and 3 o'clock are the hands of the clock opposite each other?
Thank you for your help..=)
Found 2 solutions by J2R2R, josmiceli:
Answer by J2R2R(94)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let us start at 12:00 when the two hands are together.
The hour hand will pass through A degrees.
The minute hand will pass through 720 degrees (2 hours) + (180 + A) degrees to be opposite the hour hand.
Since the minute hand travels 12 times as fast as the hour hand,
12A = 720 + 180 + A
11A = 900
A = 81 + 9/11
Which is 21 + 9/11 into the third hour since the first two hours take up 60 degrees.
The hour hand will have passed through 21 + 9/11 degrees since 2 o’clock, it is twice this amount in minutes past 2 o’clock since the hour hand takes 60 minutes to pass through 30 degrees (2 minutes per degree).
Therefore the time is 43 + 7/11 minutes past 2 o’clock.
We can verify this by calculating the proportions of the hour the hands have moved through in degrees with respect to an hour.
i.e. (21 + 9/11)/30 = (180 + 60 + 21 + 9/11)/360 = 8/11
180 is to be opposite, 60 is for the two hours and 21 + 9/11 is A.
Time is 2:43:38 + 2/11 of a second.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The minute hand and the hour hand are each going in
a circle at a certain speed in degrees/hr
Between 2 and 3 o'clock, the hour hand covers 5 minutes
of the 60 minutes on the clock face
 , so if the whole face is 360 degrees , so if the whole face is 360 degrees
 degrees degrees
When the hour hand moves 30 degrees, the minute and
goes all the way around, or 360 degrees. That's 12 times
faster than the hour hand
-------------------
To solve the problem, I ask the question:
If the hour hand moves a certain number of degrees be
tween 2 and 3, what time is it when the minute hand is
at the hour hand's position + 180 degrees? That would put
them directly opposite eachother.
-------------------
Let  = the elapsed time in hours after 2 o'clock when the hands = the elapsed time in hours after 2 o'clock when the hands
are opposite eachother
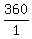 = the rate of travel of the minute hand in degrees/ hr = the rate of travel of the minute hand in degrees/ hr
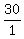 = the rate of travel of the hour hand in degrees/hr = the rate of travel of the hour hand in degrees/hr
--------------------
Reading from 12 and going clockwise, the hour hand is at the 2
which is  of the 360 degrees of the 360 degrees
 degrees degrees
So, when the hands are opposite the hour hand is at
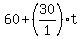
I want the minute hand to be this position + 180 degrees.
I also know that 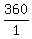 { is the minute's hand rate of travel) { is the minute's hand rate of travel)
so, I can write



 hrs hrs
 min min
 min min
and
 sec sec
The hands are opposite eachother at 43 min and 38 sec past 2 o'clock
---------------------
check answer:
In degrees the hour hand has moved
 degrees degrees
In degrees, the minute hand has moved
 degrees degrees
 degrees degrees
If I subtract the 60 degree headstart the hour hand had,

|
|
|