SOLUTION: 12. Al and Ruby each roll ordinary dice once. What’s the probability that the number of Ruby’s roll is greater than the number of Al’s roll ?

Algebra ->  Test -> SOLUTION: 12. Al and Ruby each roll ordinary dice once. What’s the probability that the number of Ruby’s roll is greater than the number of Al’s roll ?      Log On


   

Question 178828: 12. Al and Ruby each roll ordinary dice once. What’s the probability that the number of Ruby’s roll is greater than the number of Al’s roll ?
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
12. Al and Ruby each roll ordinary dice once. What’s the probability that the number of Ruby’s roll is greater than the number of Al’s roll ?

Here is the sample space of 36 possibilities,
where in each parentheses the number on the left
is Al's roll and the number on the right is Ruby's. 


(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)   

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

Now I will color all the ones red which
are successful, that is, where Ruby's roll
is greater than Al's:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) 

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

There are 15 successful (red) cases out of the 36.

Therefore the desired probability is 15%2F36 which
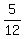reduces to 5%2F12.

Edwin