Question 1210504: If A and B are positive 2 digest integers, how many solutions are there of the equation 2a+3b=100
Found 4 solutions by MathLover1, ikleyn, math_tutor2020, greenestamps:
Answer by MathLover1(20854)   (Show Source):
Answer by ikleyn(53354)  (Show Source):
You can put this solution on YOUR website! .
If 'a' and 'b' are positive  2-digit integers,
how many solutions are there of the equation 2a+3b=100.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The post by @MathLover1 isn't a solution to the problem because it doesn't answer the problem's question.
The question "how many" remains unanswered, or she shifts the calculation to the reader.
Therefore, her post is a talk about a solution, but not the solution itself.
I came to deliver the solution as it should be.
In equation
2a + 3b = 100,
the term '2a' is an even number and right side '100' is an even number, too.
Hence, the term '3b' must be even number. It implies that number 'b' must be even number.
Then '3b' is a multiple of 6.
Thus, '3b' should be multiple of 6 and 'b' itself should be a two-digit positive integer number.
The smallest such number '3b' is 30.
So, the numbers '3b' form the set < 30, 36, 42, . . . >.
We want to determine the maximum possible value of '3b'.
It should allow 'a' in equation '2a = 100 - 3b' to be a 2-digit positive integer number.
So, the greatest possible value of '3b' is not more than 80.
Thus, our set for '3b' is the sequense < 30, 36, 42, . . . , 78 >.
It contains 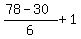 = 9 numbers.
So, equation 2a + 3b = 100 has 9 solutions in positive integer numbers (a,b),
such that 'a' and 'b' are 2-digit positive integer numbers.
ANSWER. There are 9 solutions under imposed conditions.
Solved.
Answer by math_tutor2020(3827)  (Show Source):
You can put this solution on YOUR website!
Answer: 9
-------------------------------------------------------------------------
Reasoning
It sounds like "digest" should be "digit".
I'm assuming the question is:
"If A and B are positive two-digit integers, how many solutions are there to the equation 2a+3b = 100?"
Let's look at the related equation 2a+3b = 1, since we can multiply both sides by 100 later.
Through fairly quick trial-and-error, you should find an integer solution is (a,b) = (-1,1)
Another method is to look at the graph of 2x+3y = 1 to find a lattice point, or you can use the Extended Euclidean Algorithm.
Since (-1,1) is a solution we can state that
2a+3b = 1
2*(-1)+3*(1) = 1
Multiply both sides by 100 to get,
2*(-1)+3*(1) = 1
100*( 2*(-1)+3*(1) ) = 100*1
100*2*(-1) + 100*3*(1) = 100
2*( 100*(-1) ) + 3*(100*1) = 100
2*( -100 ) + 3*(100) = 100
This demonstrates that (a,b) = (-100,100) is an integer solution to 2a+3b = 100.
Unfortunately a = -100 is not positive, and it's not a two-digit number either.
A similar problem shows up with b as well.
We must require that 10 <= a <= 99 and 10 <= b <= 99.
The symbol <= means "less than or equal to".
2x+3y = 100 solves to y = (-2/3)x+(100/3)
The slope -2/3 will tell us how to go from one integer point to another on this line.
Start at (-100,100).
Move down 2, right 3 to arrive at (-97,98)
Move down 2, right 3 to arrive at (-94,96)
etc
This "down 2, right 3" pattern can be expressed like this
a = -100+3t
b = 100-2t
where t is an integer.
If t = 0, then it leads to (a,b) = (-100,100)
If t = 1, then it leads to (a,b) = (-97,98)
If t = 2, then it leads to (a,b) = (-94,96)
and so on.
If t was negative, then you go the opposite direction "up 2, left 3".
Then,
10 <= a <= 99
10 <= -100+3t <= 99
10+100 <= -100+3t+100 <= 99+100
110 <= 3t <= 199
110/3 <= 3t/3 <= 199/3
36.67 <= t <= 66.33 approximately
Since t is an integer we round the lower bound up to the nearest integer; while the upper bound gets pulled down to the nearest integer.
Note how t = 36 is too small since it leads to a = 8; while t = 67 is too large because it leads to a = 101.
Anyways, we go from
36.67 <= t <= 66.33
to
37 <= t <= 66
Meanwhile,
10 <= b <= 99
10 <= 100-2t <= 99
10-100 <= 100-2t-100 <= 99-100
-90 <= -2t <= -1
-90/(-2) >= -2t/(-2) >= -1/(-2) .... inequality signs flip
45 >= t >= 0.5
0.5 <= t <= 45
1 <= t <= 45 .... rounding to nearest integer
The inequality signs flipped because we divided all sides by a negative number.
Overlap these two intervals
37 <= t <= 66
1 <= t <= 45
To get the interval 37 <= t <= 45
I recommend drawing out a number line.
This set of t values will make both 10 <= a <= 99 and 10 <= b <= 99 true simultaneously where a = -100+3t and b = 100-2t.
How many integers are in the set {37,38,...,45}?
We want the 37 to go to 1, the 38 to go to 2, etc.
Subtract 36 from each item and you'll get the set {1,2,...,9}
Or you could say 45-37+1 = 9
The formula I used is that there are n-m+1 items in the set {m,m+1,m+2,...,n-1,n} where m,n are integers and m < n.
Note the -37+1 portion combines to -36, which is what we subtracted from each item of the previous set.
We determined there are 9 integer solutions to the equation 2a+3b = 100 where a,b are positive two-digit integers.
Using a spreadsheet, or something like Python, the set of all solutions we're after is this
a = 11, b = 26
a = 14, b = 24
a = 17, b = 22
a = 20, b = 20
a = 23, b = 18
a = 26, b = 16
a = 29, b = 14
a = 32, b = 12
a = 35, b = 10
Each time 'a' goes up by 3, b drops by 2.
It seems like your teacher only cares about the number of solutions, rather than the solutions themselves. So this portion is likely optional.
Answer by greenestamps(13250)  (Show Source):
You can put this solution on YOUR website!
This is a linear Diophantine equation -- one equation with two variables, with a finite number of solutions because the solutions are positive integers. A common start on finding the set of solutions is to solve the equation for one variable.
Because the numbers 2 and 100 are both even, it is probably fastest to solve the given equation for b.
 [1]
With the equation in the last form [1], we see that (50-a) must be divisible by 3. That means, among other things, that consecutive values of a that provide solutions will differ by 3.
(1) Solution with smallest value of a...
Remembering that the solutions must have both a and b positive 2-digit integers, we can see that the smallest 2-digit value for a that makes (50-a) divisible by 3 is 11.
That gives us 
(2) Solution with the largest value of a...
The solution with the largest value of a is the one with the smallest value of b. Again since a and b must be 2-digit integers, equation [1] says that all values of b that give solutions will be even, so the smallest value of b that will give a solution is the smallest 2-digit even integer, which is 10.
From (1) and (2), the solutions are the ones with b having even values from 10 to 26 inclusive. The number of such solutions is
ANSWER: There are 9 solutions having both a and b 2-digit positive integers
|
|
|
