Question 1210429: 1) Solve 2(√4x+5) - (√3x+1) = 6, where x is an integer.
2) Given that sinx = -3/5, where 180° ≤ x ≤ 270° and cos y = - 15/17 , where 90° ≤ y ≤ 180°. find the value of tan(x-y).
Found 3 solutions by ikleyn, greenestamps, n2:
Answer by ikleyn(53354)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) Solve 2(√4x+5) - (√3x+1) = 6, where x is an integer.
2) Given that sinx = -3/5, where 180° ≤ x ≤ 270° and cos y = - 15/17 , where 90° ≤ y ≤ 180°.
find the value of tan(x-y).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve here problem (2), ONLY.
Since sin(x) = -3/5 in QIII, it implies cos(x) =  = -4/5.
Since cos(y) = -15/17 in QII, it implies sin(y) = = -4/5.
Since cos(y) = -15/17 in QII, it implies sin(y) = 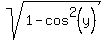 = 8/17.
Therefore tan(x) = = 8/17.
Therefore tan(x) = 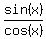 = = 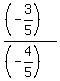 = 3/4,
tan(y) = = 3/4,
tan(y) =  = = 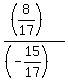 = -8/15.
Now apply the formula for tan(x-y)
tan(x-y) = = -8/15.
Now apply the formula for tan(x-y)
tan(x-y) = 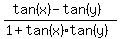 .
In the numerator, we have
tan(x) - tan(y) = .
In the numerator, we have
tan(x) - tan(y) = 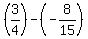 = = 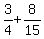 = = 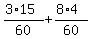 = = 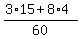 = =  .
In the denominator, we have
1 + tan(x)*tan(y) = .
In the denominator, we have
1 + tan(x)*tan(y) = 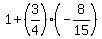 = = 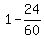 = = 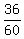 .
Thus finally tan(x-y) = .
Thus finally tan(x-y) = 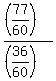 = =  .
ANSWER. tan(x-y) = .
ANSWER. tan(x-y) =  . .
Part (2) is completed.
Never pack more than one problem in every post.
It is the rule and the policy of this forum,
and also the rule and the policy of every other similar forum.
( and, in general, the rule of polite communication between people. )
Whether you follow this rule or not shows
whether you treat the people you are addressing with respect or not.
Answer by greenestamps(13250)   (Show Source): (Show Source):
Answer by n2(19)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) Solve 2(√4x+5) - (√3x+1) = 6, where x is an integer.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Tutor @greenestamps made a great step forward, guessing or finding mentally
one integer solution x = 5.
But when a solution to a Math problem, or a math equation is found by the " trial and error "
guessing method, always a question arises - whether this solution is unique or whether other solutions exist.
There is one brilliant reasoning, which may help in some cases,
and it will help to answer for this given equation.
Notice that in the left side of the equation the term 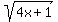 grows FASTER than grows FASTER than
the other term,  . (This is obvious). . (This is obvious).
AFORTIORI, the term  grows even FASTER than the other term, grows even FASTER than the other term,  . .
It means that the left side of the given equation is a monotonic function of x
(monotonically increases for positive values of x).
Hence, this given equation, having a constant value in its right side, has a UNIQUE solution.
In other words - if it has one solution, then this solution is unique.
Reasoning this way, we transform our " trial and error " guessing method into MATHEMATICALLY STRICT  . .
So, x = 5 is the unique real and integer solution to this given equation.
Z Z Z !
Be careful ! That is true that in the positive 'x'-domain the left side monotonically increases.
But what about negative 'x' ? - In this problem, the domain of negative 'x' is small and does not
make influence to the final conclusion !
|
|
|