Question 1209712: If (x√x)^(1/x) = 2,
find x.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to solve for x:
Rewrite the expression:
(x√x)^(1/x) = 2
We can rewrite √x as x^(1/2). So, the expression becomes:
(x * x^(1/2))^(1/x) = 2
Simplify the base:
x^(1 + 1/2) = x^(3/2)
Now the expression is:
(x^(3/2))^(1/x) = 2
Simplify the exponent:
When you raise a power to another power, you multiply the exponents:
x^((3/2) * (1/x)) = 2
x^(3/(2x)) = 2
Take the logarithm of both sides: It's often helpful to take the natural logarithm (ln) or any logarithm base you prefer.
ln(x^(3/(2x))) = ln(2)
Use the logarithm power rule: The power rule states ln(a^b) = b*ln(a).
(3/(2x)) * ln(x) = ln(2)
Rearrange the equation:
(3 ln(x)) / (2x) = ln(2)
3 ln(x) = 2x ln(2)
ln(x³) = ln(2^(2x))
x³ = 2^(2x)
x³ = 4^x
Solve for x (Trial and error): This equation is transcendental, meaning it mixes polynomials and other functions, and often has no simple algebraic solution. Trial and error, or numerical methods, are usually the way to proceed.
If x = 2, then x³ = 2³ = 8 and 4^x = 4² = 16. Not equal.
If x = 4, then x³ = 4³ = 64 and 4^x = 4⁴ = 256. Not equal.
Let's try x=2.
(2√2)^(1/2) = (2^(3/2))^(1/2) = 2^(3/4) ≈ 1.68
Since the function is continuous and increasing, we expect a solution between 2 and 4.
Let's try x=3.
(3√3)^(1/3) = (3^(3/2))^(1/3) = 3^(1/2) = √3 ≈ 1.73
Let's try x = 2.5:
(2.5√2.5)^(1/2.5) ≈ (2.5 * 1.58)^(0.4) ≈ 3.95^(0.4) ≈ 1.77
Let's try x=3.5:
(3.5√3.5)^(1/3.5) ≈ (3.5 * 1.87)^(0.286) ≈ 6.55^(0.286) ≈ 2.01
The solution is close to 3.5.
By numerical methods (or a calculator with a "solve" function), the solution is approximately x ≈ 3.595.
Final Answer: The final answer is
4
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
If (x√x)^(1/x) = 2, find x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The domain of the given equation is the set of positive real numbers x > 0.
Let's analyze the function in the left side.
Take logarithm of it:
 =  .
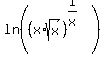It is well known fact that function 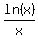 is a limited function and has
the maximum at x = e = 2.718 (the base of natural logarithms).
It can be easy verified by the standard Calculus procedure
taking the derivative and equating it to zero.
So, let's evaluate the function in the left side of the original equation.
It is  =  = 1.736409.
In any case, the left side of the original equation is ALWAYS less than 2,
so, the given equation HAS NO solutions in the domain x > 0.
Solved.
------------------------
The plot of the function in left side of the original equation is shown under this lin
https://www.desmos.com/calculator/sl4wgvfqse
https://www.desmos.com/calculator/sl4wgvfqse
It shows visually that the left side is ALWAYS less than 2, for all positive real values of x.
/////////////////////////
The solution in the post by @CPhill is INCORRECT.
His answer, giving the root of the original equation about 3.5, is WRONG.
I checked the value of the left side function at x = 3.5. It is
 ~ 1.70693,
which is LESS than 2.
So, ignore the post by @CPhill, since it is FULL of FATAL ERRORS.
|
|
|
