Question 1209571: If x⁵ = 1 with x ≠ 1
find the value of
1/(1+x²) + 1/(1+x⁴) + 1/(1+x) + 1/(1+x³)
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
If x⁵ = 1 with x ≠ 1, find the value of
1/(1+x²) + 1/(1+x⁴) + 1/(1+x) + 1/(1+x³)
~~~~~~~~~~~~~~~~~~~~
In this problem, all numbers  , for which x^5 = 1, are five different complex roots of equation
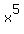 = 1, k = 1, 2, 3, 4, 5. (1)
including real root x = 1.
THREFORE, the numbers 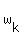 =  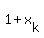are the five complex roots of equation
 = 1. (2)
including real number w = 2, which corresponds to real numer 1, which is the root of (1).
Hence, the reciprocal numbers 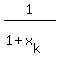 are the roots of this equation
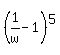 = 1. (3)
including real number w = 1/2, which corresponds to real numer 1, which is the root of (1).
Equation (3) can be written in equivalent polynomial form
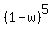 = w^5. (4)
or
1 - 5w + 10w^2 - 10w^3 + 5w^4 - w^5 = w^5,
or
2w^5 - 5w^4 + 10w^3 - 10w^2 + 5w - 1 = 0. (5)
So, the sum of four addends
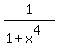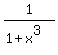 +  +  +  (6)
is the sum of all four complex roots of equation (5), that are not real numbers.
Let's add  to the sum (6). We will get the sum S
S = + + + + 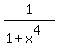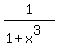. (7)
Now this sum (7) is the sum of all complex roots of equation (5).
According to Vieta's theorem, this sum (7) is the coefficient at  divided by the coefficient at x^5
of equation (5), taken with the opposite sign.
This ratio of the mentioned coefficients in (5) is  =  .
Hence, the sum (7) is equal to - =  .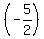
But the problem asks about S - , and we finally find this value
S - = + + 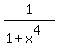+ 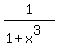= - =  = 2.
At this point, the problem is solved completely, to the very end.
ANSWER. If x⁵ = 1 with x ≠ 1, then the sum 1/(1+x²) + 1/(1+x⁴) + 1/(1+x) + 1/(1+x³) is 2.
Solved.
This problem/solution is of the MOST UPPER LEVEL of the problems of this kind.
By the way, my solution shows that the problem can be generalized
for more high degrees in equation (1) and more longer sums
with the similar expressions for the roots.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Answer: 2
Explanation
We can pair up these two terms to get:
1/(1+x) + 1/(1+x^4)
= (1+x^4)/( (1+x)(1+x^4) ) + (1+x)/( (1+x)(1+x^4) )
= (1+x^4+1+x)/(1+x^4+x+x^5)
= (x^4+x+2)/(1+x^4+x+1) ..... use x^5 = 1
= (x^4+x+2)/(x^4+x+2)
= 1
Through similar steps,
1/(1+x^2) + 1/(1+x^3) = (x^3+x^2+2)/(x^5+x^3+x^2+1)
Plug in x^5 = 1 then you'll have it simplify to,
(x^3+x^2+2)/(x^5+x^3+x^2+1)
= (x^3+x^2+2)/(1+x^3+x^2+1)
= (x^3+x^2+2)/(x^3+x^2+2)
= 1
We determined that
1/(1+x) + 1/(1+x^4) = 1 when x^5 = 1
1/(1+x^2) + 1/(1+x^3) = 1 when x^5 = 1
Adding those results gets to the final answer of 2.
--------------------------------------------------------------------------
Another approach:
x^5 = 1 can be solved using the roots of unity formula
See this link for more info
https://artofproblemsolving.com/wiki/index.php/Roots_of_unity
One of the five roots is x = 1, but we cannot use it since the instructions state as such.
But you can use any of the four complex roots of the form a+bi.
Let's say those four roots are p,q,r,s
If you select a complex root at random, say p, then you can compute 1/(1+p^2)+1/(1+p^4)+1/(1+p)+1/(1+p^3) by using a calculator.
The result my calculator says is roughly 2+9.9836*10^(-13)*i
The 9.9836*10^(-13) portion is so very small that it is basically zero. This is due to rounding error.
So we really have 2+0i or simply 2 as the final answer.
|
|
|
