Question 1209554: Simplify
(89 + 28√10)^(¼) = √a + √b
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Simplify (89 + 28√10)^(¼) = √a + √b.
~~~~~~~~~~~~~~~~~~~
First, it is easy to see that
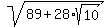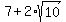 =  . (1)
Indeed, if you square right side of (1), you will get  .
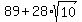Thus, equality (1) is proved.
Second,
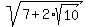 =  +  . (2)
Indeed, if you square right side of (2), you will get  .
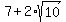Thus, equality (2) is proved.
Equalities (1) and (2) combined mean that
 = + .
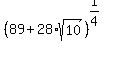QED. So, a= 5, b= 2.
Solved.
This problems teaches to extract MENTALLY square roots of the form
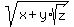 with integer x, y, z, as they are in this assignment.
Answer by greenestamps(13200)  (Show Source):
|
|
|
