SOLUTION: On the number line x= 2/9 and y= 17/18. The point z divides the segment from x to y into two parts such that the distance from x to z is 5/9 of the distance from z to y. Find the d

As you read the problem, write this equation

     = .


This equation is the literal translation of the words to Math.

To solve, multiply both sides by 9.  You will get

    9z - 2 = .


Multiply both parts of the last equation by 18.  You will get

    162z - 36 = 5*17 - 5*18z,

    162z - 36 = 85 - 90z,

    162z + 90z = 85 + 36,

    252z = 121,

       z = .


The distance from z to y is   =  =  =  = .


ANSWER.  The distance from z to y is  .

On the number line x= 2/9 and y= 17/18. The point z divides the segment from x to y into two parts such that the distance from x to z is 5/9 of the distance from z to y. Find the distance from z to y.

To keep things uniform, let's change x to match y's denominator, 18. We than get x as:  
Distance between x and y:  
With point z between xy, we get segments, xz, and zy, with xz + zy = xy ===> xz = xy - zy 
As distance from x to z is 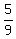 the distance from z to y, 
                                                     -- Substituting xy - zy for xz 
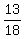                                                     ----- Substituting  for xy
                                                  13 - 18zy = 10zy ----- Multiplying by LCD, 18
                                                         13 = 10zy + 18zy
                                                         13 = 28zy
                          Distance from z to y, or 

It would seem a lot less complex - if it's considered so now - to draw a number line in 18s,
i.e. , and marking off points x, y, and z, so this can be clearer to you.