Question 1207391: A paper cone of circular base diameter 10cm and height 12cm, is flattened out into the sector of a circle, what is the angle of the sector?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A paper cone of circular base diameter 10cm and height 12cm, is flattened out
into the sector of a circle, what is the angle of the sector?
~~~~~~~~~~~~~~~~~~~
This problem is nice.
Solving it step by step, I will try to explain you why it is so.
When we flatten out a cone into the sector of a circle,
the radius of this circle is the slant height of the cone,
while the arc of this sector is the circumference of the base circle of the cone.
So, we should find the slant height and the circumference of the base circle.
The slant height is the hypotenuse of the right triangle, whose legs are
the radius of the base circle and the height of the cone.
So, in our case, the slant height is
h = 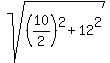 = =  = = 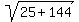 = =  = 13 cm.
The circumference of the base circle is
C = = 13 cm.
The circumference of the base circle is
C = 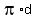 = = 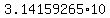 = 31.4159265 cm (approximately).
Now the angle of the sector = 31.4159265 cm (approximately).
Now the angle of the sector  is connected with the slant height and the arc length
by equation
C = is connected with the slant height and the arc length
by equation
C = 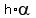 ,
where ,
where  is in radians. Here "h" plays the role of the radius of the arc.
So, we find is in radians. Here "h" plays the role of the radius of the arc.
So, we find
 = = 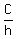 = = 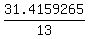 = 2.416609731 radians.
If you want to have it in degrees, convert radians to degrees = 2.416609731 radians.
If you want to have it in degrees, convert radians to degrees
 = = 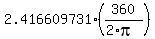 = = 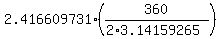 = 138.4615 degrees (approximately).
ANSWER. The angle of the sector is about 2.416609731 radians or 138.4615 degrees. = 138.4615 degrees (approximately).
ANSWER. The angle of the sector is about 2.416609731 radians or 138.4615 degrees.
At this point, the problem is solved in full.
-----------------
The problem is nice, because different conceptions of geometry play together to provide the solution.
|
|
|