Question 1206940: Calculate the 95% margin of error in estimating a population mean 𝜇 for the following values. (Round your answer to three decimal places.)
n = 30, 𝜎2 = 0.3
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you want the margin of error for a 95% confidence interval.
n = 30 = sample size
s^2 = .3 = variance.
s = standard deviation = sqrt(.3).
standard error = s / sqrt(30) = sqrt(.3) / sqrt(30) = .1.
critical z-score at 95% two tail confidence interval is plus or minus 1.96.
margin of error is calculated from the high side of the confidence interval.
it can be calculated from either side, but it will be the same.
on the high side of the confidence interval it is added to the mean.
on the low side of the confidence interval it is subtracted from the mean.
z = (x-m) / s is the z-score formula.
for this problem:
z = plus or minus 1.96
(x-m) is the margin of error.
s is the standard error.
note that s is sometimes use for the standard deviation and sometime used for the standard error.
to make it even more confusing, the calculators will show the box where you fill in the standard error as the standard deviation box.
note that the standard error is defined as the standard deviation of the distribution of sample means.
it's still a standard deviation, but it's the standard deviation of the distribution of sample means rather than the standard deviation of individual scores.
formula becomes 1.96 = (x-m) / .1
solve for (x-m) to get (x-m) = .1 * 1.96 = .196.
in this type of problem, the mean can be anything as long as the standard error remains the same.
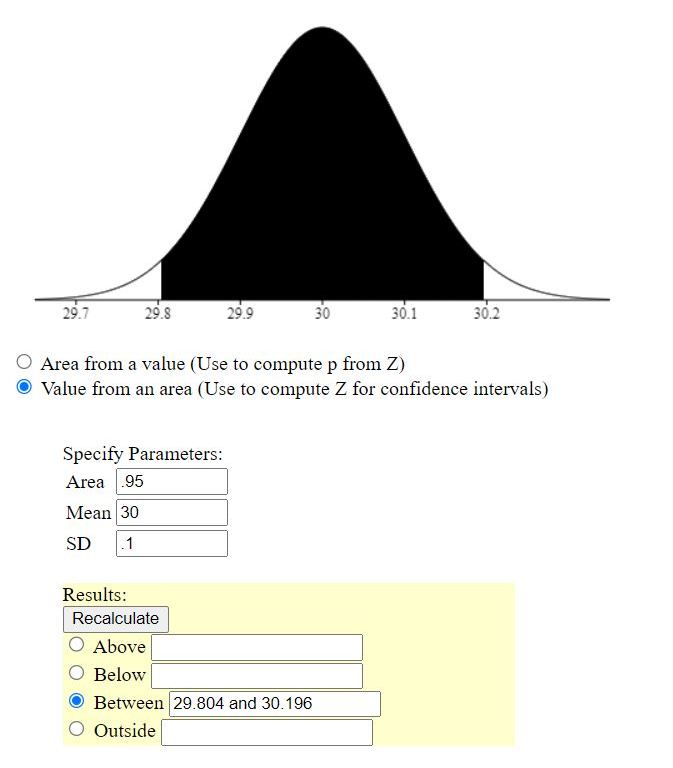
for example, if the mean is 30 (chosen randomly), then your 95% confidence interval becomes 29.804 to 30.196.
the margin of error is .196 as we had calculated earlier.
above the mean, the threshold is 30 + .196 = 30.196.
below the mean, the threshold is 30 - .196 = 29.804.
this is what it looks like on a normal distribution graph.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
At 95% confidence, the z critical value is roughly z = 1.96
This value is to be memorized or looked up in a reference table.
sigma = population standard deviation
sigma^2 = population variance = 0.3
sigma = sqrt(0.3)
E = margin of error for the mean
E = z*sigma/sqrt(n)
E = 1.96*sqrt(0.3)/sqrt(30)
E = 0.196 is the approximate margin of error
|
|
|