We seek to find a simpler form 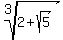 }
We try to find a simpler expression of the same form as what's
under the radical, namely a surd of the form
}
We try to find a simpler expression of the same form as what's
under the radical, namely a surd of the form  , where
a and b are rational numbers.
If this is possible, then
, where
a and b are rational numbers.
If this is possible, then
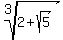

 Cubing both sides:
Cubing both sides:



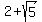

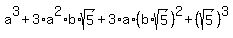
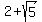

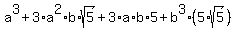
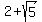

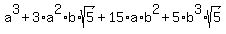 The rational terms on the left must equal the rational terms on the right,
and The irrational terms on the left must equal the irrational terms on the
right, so we have this system
The rational terms on the left must equal the rational terms on the right,
and The irrational terms on the left must equal the irrational terms on the
right, so we have this system
 Eliminate the constants by multiplying the 2nd equation by -2
Eliminate the constants by multiplying the 2nd equation by -2
 Adding the equations:
Adding the equations:
 Notice that the coefficients have sum 1-6+15-10 = 0.
That means a=b is a solution. Substituting a for b,
Notice that the coefficients have sum 1-6+15-10 = 0.
That means a=b is a solution. Substituting a for b,




 Taking cube roots of both sides:
Taking cube roots of both sides:
 and since a=b,
and since a=b,
 becomes
becomes
 Edwin
Edwin