Question 1205605: Let f(x) = (6+7x)/(2-x)(1+x^2)
(i) Express f(x) in partial fractions.
(ii) Show that, when x is sufficiently small for x^4 and higher powers to be neglected,
f(x) = 3 + 5x - (1/2 x^2) - (15/4 x^3)
Answer by ikleyn(52747)   (Show Source):
You can put this solution on YOUR website! .
Let f(x) = [(6+7x)/(2-x)(1+x^2)]
(i) Express f(x) in partial fractions.
~~~~~~~~~~~~~~~~~~~
f(x) has this decomposition in partial fractions
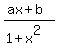 =  +  . (1)
with some real coefficients "a", "b" and "c".
These coefficients are unknown now, and the rest part of this post is to determine them.
Multiply both sides of equality (1) by 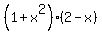 . You will get
6 + 7x = (ax+b)*(2-x) +  . (2)
At x= 2, equation (2) gives
6 + 7*2 = c*(1+2^2), or 20 = 5c, or c= 20/5 = 4.
At x= 0 and c= 4, equation (2) gives
6 + 7*0 = (a*0+b)*(2-0) + 4*(1+0^2), or 6 = 2b + 4; then 6-4 = 2b, 2 = 2b, b = 2/2 = 1.
At x= 1 and c= 4, b= 1, equation (2) gives
6 + 7*1 = (a*1+1)*(2-1) + 4*(1+1^2), or 13 = (a+1) + 4*2; then 13 - 8 = a+1; 5 = a+1; a= 5-1 = 4.
ANSWER. =  +  .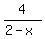
Part (1) is solved.
|
|
|
