SOLUTION: A circle and a cone are inside a cylinder and the diameters and heights of the solids are equal. a) What fraction of the volume of the cylinder is i) the sphere ii) the cone?

A circle is a plane figure, not a solid. Then in (a)i),

you ask about a sphere but you haven't mentioned a sphere 
at all. Maybe you meant "sphere" and wrote "circle" by 
mistake. But if the cone has the same diameter and height 
then it reaches from top to bottom of the cylinder, and
there would be no room for a sphere of the same diameter. 
So both the cone and a sphere of the same diameter and 
height could not fit inside a cylinder at the same time. 
Here are some formulas you might use to figure out what 
you want. 

The volume of a cylinder is , 
The volume of a cone is 
The volume of a sphere is 
The surface area of a cylinder open at each end is
, closed with a circle at either end adds
a circle of area  each.
The surface area of a cone open at the top is 
, where l = the slant height. Closed at the
top adds a circle .

Also, the ratio of X to Y is 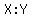 or 

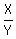Your problem is not clear.  You might consider reposting
your problem. Be sure to copy it EXACTLY AS IT IS WRITTEN
this time.

Edwin