SOLUTION: The angle of depression of a point on the 225m contour line is 10.2° from the top of a hill 915m high. Calculate the horizontal distance between the two points. Find the differe

In vertical section, you have a right-angle triangle with vertical leg of 915-225 = 690 meters
(the difference of the levels).

Its other, horizontal leg, is the unknown horizontal distance d.


You have this equality for tangent of the given angle 10.2° 

    tan(10.2°) = ,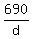


which gives you  d = 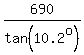 =  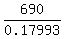= 3835 meters (approximately).


        So, the horizontal distance is about 3835 meters.


The distance D along the hillside is the hypotenuse of our right-angle triangle, so

    sin(10.2°) = ,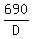


which gives you D = 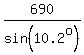 =  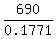= 3896 meters (approximately).


        So, the distance along the hillside is about 3896 meters.


The difference between the two distances is  3896 - 3835 = 61 meters.