.
Topic : Discrete Random Variable (Geometric Distribution)
A coin is biased such that the probability of obtaining heads with each toss is equal to 5/11.
The coin is tossed until the first head is obtained. Find the probability that the coin is tossed:
(a) At least six times
(b) Fewer than eight times
~~~~~~~~~~~~~~~~~
(a) "At least six times" in this problem means that coin can be tossed
6 or more times until the first head is obtained (i.e. the first head is obtained
at 6th, or 7th, or 8th and so on toss).
It gives us an infinite sequence of disjoint events
1st 2nd 3rd . . .
TTTTTH TTTTTTH TTTTTTTH . . .
where "T" denotes "tail" and "H" denotes "head".
The probability is an infinite sum of these terms
P = 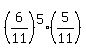 +
+ 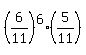 +
+ 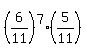 + . . .
It is the sum of a geometric progression with the first term a=
+ . . .
It is the sum of a geometric progression with the first term a= 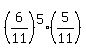 and the common ratio
and the common ratio  .
Hence, the infinite sum is
P =
.
Hence, the infinite sum is
P =  =
=  =
= 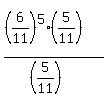 =
= 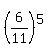 . ANSWER to question (a)
(b) "Fewer than eight times" in this problem means that coin can be tossed 0 times, or 1 time, or 2 times,
or 3 times, . . . , or 7 times until the first head is obtained (i.e. the first head is obtained
at 0th, or 1st, or 2nd and so on toss).
It gives us a finite sequence of disjoint events
1st 2nd 3rd 4th . . . 7th
H TH TTH TTTH . . . TTTTTTH
where "T" denotes "tail" and "H" denotes "head".
The probability is a finite sum of these terms
P =
. ANSWER to question (a)
(b) "Fewer than eight times" in this problem means that coin can be tossed 0 times, or 1 time, or 2 times,
or 3 times, . . . , or 7 times until the first head is obtained (i.e. the first head is obtained
at 0th, or 1st, or 2nd and so on toss).
It gives us a finite sequence of disjoint events
1st 2nd 3rd 4th . . . 7th
H TH TTH TTTH . . . TTTTTTH
where "T" denotes "tail" and "H" denotes "head".
The probability is a finite sum of these terms
P = 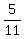 +
+ 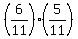 +
+ 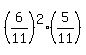 + . . . +
+ . . . + 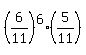 .
It is the sum of first 7 terms of a geometric progression with the first term a=
.
It is the sum of first 7 terms of a geometric progression with the first term a= 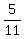 and the common ratio r =
and the common ratio r =  .
Hence, the sum is
P =
.
Hence, the sum is
P =  =
= 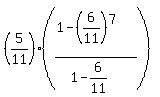 =
=  =
=  . ANSWER to question (b)
Notice that this final probability is the complement of
. ANSWER to question (b)
Notice that this final probability is the complement of  to 1, as it is should be,
so this solution is correct.
to 1, as it is should be,
so this solution is correct.
Solved.