Question 1203284: A staff car park at a school has 13 parking spaces in a row.
There are 9 cars to be parked.
a. In how many different arrangements are there for parking the 9 cars and leaving 4 empty spaces?
b. How many different arrangements are there if the 4 empty spaces are next to each other?
c. If the parking is random, find the probability that there will not be 4 empty spaces next to each other.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(a) One way to think of the problem is with 13 letters in a row, with 9 "F" representing the parking spaces that are full and 4 "E" representing the spaces that are empty. Then by a well-known counting principle the number of possible arrangements is

ANSWER: 715
Note another way to look at the problem is simply choosing 9 of the 13 spaces to be the ones that get used. Then the calculation is

Of course the answer (and the calculation that was made) is the same.
(b) In the case where the 4 empty spaces are together, think of the parking spaces as being numbered 1 to 13; then the first of the four empty spaces can be space number 1, number 2, ..., or number 10. So there are 10 arrangements in which the four empty spaces are together.
ANSWER: 10
(c) There are 715 total arrangements, of which 10 have the four empty spaces together, so 705 arrangements have the empty spaces not all together. So the probability that the four empty spaces will not be together is 705/715.
ANSWER: 705/715 = 141/143
Convert to decimal or percent if desired/required.
Answer by ikleyn(52866)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A staff car park at a school has 13 parking spaces in a row.
There are 9 cars to be parked.
a. In how many different arrangements are there for parking the 9 cars and leaving 4 empty spaces?
b. How many different arrangements are there if the 4 empty spaces are next to each other?
c. If the parking is random, find the probability that there will not be 4 empty spaces next to each other.
~~~~~~~~~~~~~~~~~~~
In my solution, I consider the cars as different / distinguishable.
Indeed, they have, at least, different license plates.
(a) We can represent each placement/arrangement of the cars in a parking
as a word of the length 13 consisting of 9 different letters and the 10th symbol,
which is a blank symbol.
Then the problem is reduced to this question:
how many words of the length 13 are there, written with 9+1 = 10
different symbols, such that one of these 10 symbols is repeating 4 times?
It is a standard model/problem of combinatorics for arranging sets with repeating elements.
Its solution is well known. The formula is
the number of arrangements is 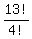 = = 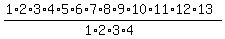 = 259,459,200. ANSWER
(b) Obviously, there are (9-1) + 1 + 1 = 10 way to place the block of 4 blank symbols
in the row of 13 positions, where 9 positions are occupied by 9 letters.
In the remaining 9 positions, 9 cars can be placed in 9! ways;
so, there are 10*9! = 10! = 10*9*8*7*6*5*4*3*2*1 = 3,628,800 different arrangements of this kind.
(c) To answer (c), we should take the ratio of the number of 10! = 3,628,800 from (a) and
the number of 259,459,200 from (b) and then to take the complement to this ratio
P = 1 - = 259,459,200. ANSWER
(b) Obviously, there are (9-1) + 1 + 1 = 10 way to place the block of 4 blank symbols
in the row of 13 positions, where 9 positions are occupied by 9 letters.
In the remaining 9 positions, 9 cars can be placed in 9! ways;
so, there are 10*9! = 10! = 10*9*8*7*6*5*4*3*2*1 = 3,628,800 different arrangements of this kind.
(c) To answer (c), we should take the ratio of the number of 10! = 3,628,800 from (a) and
the number of 259,459,200 from (b) and then to take the complement to this ratio
P = 1 - 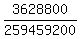 = 0.9860 (rounded). ANSWER = 0.9860 (rounded). ANSWER
Solved.
|
|
|