Question 1202117: Consider the function f(x)=2x6−12x4.
The x-intercepts occur at x=
NOTE: If there are more than one, separate your answers by a comma.
There a y-intercept at y=
To analyze the shape of the graph of f it helps to separate the domain into disjoint open intervals
(−∞,A),(A,B),(B,C),(C,D),(D,E), and (E,∞)
whose endpoints
A
are critical points of f or f′. Inside each interval there are no critical points of f or f′, so f′ and f″ cannot change sign inside the interval.
A=
B=
C=
D=
E=
For each of the intervals listed below, select the curve best representing the shape of the graph of f on that interval.
On (−∞,A):
?
On (A,B):
?
On (B,C):
?
On (C,D):
?
On (D,E):
?
On (E,∞):
?
1 2
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x)=2x^6-12x^4=2x^4(x^2-6)
x intercepts are where y=0 and they would be x=0 and x=+/- sqrt(6), so -sqrt(6),0, sqrt(6)
y intercept at the origin.
graph is 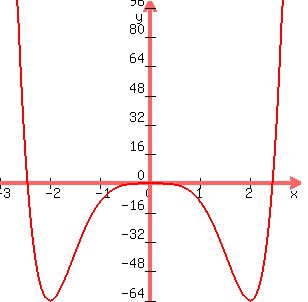
critical points: get the derivative and set equal to 0.
So 12x^5-48x^3=0=12x^3(x^2-4)=0, and critical points are at -2,0,2
The intervals that can be seen are (-oo,-sqrt(6))/// (-sqrt(6),-2)/// (-2,0)/// (0,2)///(2, sqrt(6))///(sqrt(6),oo)
See if that helps.
|
|
|