Question 1201515: You have $500,000 saved for retirement. Your account earns 7% interest. How much will you be able to pull out each month, if you want to be able to take withdrawals for 20 years?
Found 3 solutions by Theo, mananth, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you will be able to pull out 3876.49 at the end of each month.
preseent value = -500,000
future value = 0
number of time periods = 20 years * 12 months per year = 240 months.
interest rate per time period = 7% / 12 = .58333333333.....% per month.
payments are received at the end of each month.
you will be able to pull out 3854.01 at the beginning of each month, if that's what you prefer.
i used the financial calculator at https://arachnoid.com/finance/
here are the results.


Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! In twenty years he will withdraw monthly
P 500 000
n=years = 20
r=Rate = 0.07
A = monthly withdrawl

Plug the values to get the answer
A =500000*( 0.07*(1.07)^20))/((1.07)^20 -1)
= 135438.956/2.86968
=$47196.5361 can be withdrawn from the account
for 20 years
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You have $500,000 saved for retirement. Your account earns 7% interest.
How much will you be able to pull out each month, if you want to be able
to take withdrawals for 20 years?
~~~~~~~~~~~~~~~~~~~~~~
The solution, the formulas and the answer in the post by @mananth are incorrect.
I came to bring a correct solution.
The problem's formulation is INCOMPLETE (is made by unprofessional Math composer).
To be complete and professional, it must say when each withdrawal is made:
at the end or at the beginning of each month.
It is logical to assume that each withdrawal is made at the beginning of each month,
so I will assume it in my solution.
Use the general formula A =  .
Here A is the initial amount at the account; W is the monthly withdrawn value;
r is the nominal monthly percentage r = 0.07/12, presented as a decimal;
p = 1 + r, and n is the number of withdrawing periods (months, in this case).
In this problem, W is the unknown; the monthly rate is r = 0.07/12 = 0.00583...
p = 1 + 0.00583 = 1.00583, the number of payment periods (= the number of months)
is n = 20*12 = 240. So, the formula takes the form
500000 = .
Here A is the initial amount at the account; W is the monthly withdrawn value;
r is the nominal monthly percentage r = 0.07/12, presented as a decimal;
p = 1 + r, and n is the number of withdrawing periods (months, in this case).
In this problem, W is the unknown; the monthly rate is r = 0.07/12 = 0.00583...
p = 1 + 0.00583 = 1.00583, the number of payment periods (= the number of months)
is n = 20*12 = 240. So, the formula takes the form
500000 = 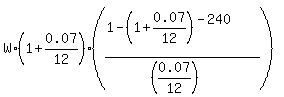 .
The factor .
The factor 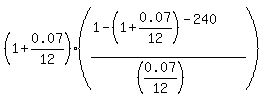 is equal to 129.7349; therefore
W = is equal to 129.7349; therefore
W = 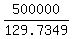 = 3854.01 dollars (rounded to the closest lesser cent).
Thus you will be able to withdraw about $3854 at the beginning of every month during 20 years. = 3854.01 dollars (rounded to the closest lesser cent).
Thus you will be able to withdraw about $3854 at the beginning of every month during 20 years.
Solved.
--------------------
In this site, there is a group of lessons associated with annuity saving plans and retirement plans. They are
- Ordinary Annuity saving plans and geometric progressions
- Annuity Due saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Withdrawing a certain amount of money periodically from a compounded saving account (*)
- Miscellaneous problems on retirement plans
From these lessons, you can learn the subject and can see many similar solved problems.
The closest lesson to your problem is marked (*) in the list.
/////////////////
In order for calculations be correct, it is recommended do not make intermediate rounding:
make rounding only at the end.
Making this kind of calculations by hands or using regular calculators is torturous.
For such purposes, people use professional calculators, or special software, or specialized online calculators.
One such calculator is referenced in the post by @Theo.
Another calculator, which you may use, is www.desmos.com/calculator.
I personally use MS Excel in my computer.
An advantage of these tools is that you can copy-paste long formulas from a computer file
directly into such calculator, and then getting an answer/(a number) is in one click.
\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the solutions by @mananth to such problems, I just saw it several times,
that his solutions were incorrect. It is not because he makes computational errors or typos.
It is because he does not know the formal computational procedure for such problems in principle.
Simply, he did not learn the subject before he decided to teach others.
So, be aware when you obtain the " solutions " from him.
|
|
|