Question 1200970: A password must be 6, 7, or 8 characters long, and may include capital letters, lower- case letters, or digits. In how many ways could this be done
A)with no restriction?
b)with no repetition permitted?
c)if at least one of the characters in part a) must be a digit?
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A password must be 6, 7, or 8 characters long, and may include capital letters,
lower-case letters, or digits. In how many ways could this be done
(a) with no restriction?
(b) with no repetition permitted?
(c) if at least one of the characters in part a) must be a digit?
~~~~~~~~~~~~~~~~~~~~~
(a) In this case, the total number of symbols is 26+26+10 = 62.
Each of these 62 symbols can be in any position, independently.
So, the number of passwords of the length 6 is 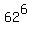 (1)
of the length 7 is (1)
of the length 7 is 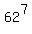 (2)
of the length 8 is (2)
of the length 8 is 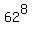 (3)
of the length 6, or 7 or 8 is the sum of number (1), (2) and (3)
N(a) = (3)
of the length 6, or 7 or 8 is the sum of number (1), (2) and (3)
N(a) = 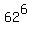 + + 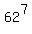 + + 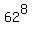 . ANSWER
(b) In this case, the total number of symbols is still the same 26+26+10 = 62.
The number of passwords of the length 6 is 62*61*60*59*58*57 (4)
of the length 7 is 62*61*60*59*58*57*56 (5)
of the length 8 is 62*61*60*59*58*57*56*55 (6)
of the length 6, or 7 or 8 is the sum of number (4), (5) and (6).
(c) To solve (c), subtract from N(a) the number of all possible passwords that do not have
digits in any position
N(c) = N(a) - . ANSWER
(b) In this case, the total number of symbols is still the same 26+26+10 = 62.
The number of passwords of the length 6 is 62*61*60*59*58*57 (4)
of the length 7 is 62*61*60*59*58*57*56 (5)
of the length 8 is 62*61*60*59*58*57*56*55 (6)
of the length 6, or 7 or 8 is the sum of number (4), (5) and (6).
(c) To solve (c), subtract from N(a) the number of all possible passwords that do not have
digits in any position
N(c) = N(a) - 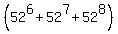 = = 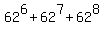 - - 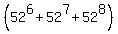 . .
Solved.
|
|
|