SOLUTION: The line (x/a) + (y/b) = 1, where a and b are positive constant, intersects the x- and y-axes at the points A and B respectively. The mid-point of AB lies on the line 2x + y = 10

Algebra ->  Test -> SOLUTION: The line (x/a) + (y/b) = 1, where a and b are positive constant, intersects the x- and y-axes at the points A and B respectively. The mid-point of AB lies on the line 2x + y = 10       Log On


   

Question 1200960: The line (x/a) + (y/b) = 1, where a and b are positive constant, intersects the x- and y-axes at
the points A and B respectively. The mid-point of AB lies on the line 2x + y = 10 and
the distance AB = 10. Find the values of a and b.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
The line x%2Fa+%2B+y%2Fb+=+1 is in intercept form with x-intercept (a,0) and 
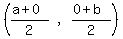y-intercept (0,b). So the midpoint of AB is %28matrix%281%2C3%2C%28a%2B0%29%2F2%2C%22%2C%22%2C%280%2Bb%29%2F2%29%29 = %28matrix%281%2C3%2Ca%2F2%2C%22%2C%22%2Cb%2F2%29%29.

Since it lies on the line 2x+%2B+y+=+10, 

2%28a%2F2%29+%2B+%28b%2F2%29+=+10,

a%2Bb%2F2=10
2a%2Bb=20
b=20-2a

Since the distance AB = 10

sqrt%28%28a-0%29%5E2%2B%280-b%29%5E2%29=10
sqrt%28a%5E2%2Bb%5E2%29=10
a%5E2%2Bb%5E2=100

a%5E2%2B%2820-2a%29%5E2=100
a%5E2%2B%28400-40a%2B4a%5E2%29=100
5a%5E2-40a=100
5a%5E2-40a-100=0
a%5E2-8a-20=0
%28a%2B2%29%28a-20%29=0
a+2=0;  a-20=0
  a=-2;    a=20
b=20-2a
b=20-2%28-2%29, b=20-2%2820%29
b=20%2B4,     b=20-20
b=24,       b=0

So at first, there seem to be two answers. The first one

a=-2, b=24

x%2F%28-2%29+%2B+y%2F24+=+1
-12x%2By=24
y=12x%2B24
with A=(a,0)=(-2,0), B=(0,24) 
and midpoint M of AB = %28matrix%281%2C3%2Ca%2F2%2C%22%2C%22%2Cb%2F2%29%29 = %28matrix%281%2C3%2C%28-2%29%2F2%2C%22%2C%22%2C%28%2824%29%29%2F2%29%29 = (-1,12)

Here is solution with a=-2, b=24. The green line is 2x + y = 10.
 

However what seemed like another solution

a=20, b=0

turned out to be extraneous because when we substitute a=20, b=0
in x%2Fa+%2B+y%2Fb+=+1, we get

x%2F20+%2B+cross%28y%2F0%29+=+1

We have an undefined term in the equation, since division by 0 is
not permitted.

If the equation had first been multiplied through by ab so that we
would have had bx%2Bay=ab then we may have had a second solution, 
but since it was given as x%2Fa+%2B+y%2Fb+=+1, the "second solution" 
was extraneous.  So there is just one solution a=-2, b=24.

Edwin