SOLUTION: The vertices of triangle ABC are A(11,3), B(2k, k) and C(-1,-11). (a) Find the two possible values of k if angle ABC is 90°. (b) Draw the diagrams to show the two possible trian

Algebra ->  Test -> SOLUTION: The vertices of triangle ABC are A(11,3), B(2k, k) and C(-1,-11). (a) Find the two possible values of k if angle ABC is 90°. (b) Draw the diagrams to show the two possible trian      Log On


   

Question 1200868: The vertices of triangle ABC are A(11,3), B(2k, k) and C(-1,-11).
(a) Find the two possible values of k if angle ABC is 90°.
(b) Draw the diagrams to show the two possible triangles
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


For angle ABC to be 90 degrees, the segments AB and BC must be perpendicular, so the product of the slopes of the two segments must be negative reciprocals.

slope of AB: (2k-3)/(k-11)
slope of BC: (2k+11)/(k+1)

%28%282k-3%29%2F%28k-11%29%29%28%282k%2B11%29%2F%28k%2B1%29%29=-1

4k%5E2%2B16k-33=-1%28k%5E2-10k-11%29

5k%5E2%2B6k-44=0

The solutions are irrational; you can use the quadratic formula to find them.

The idea of the problem is good; however, it would have been far more educational if the solutions had been rational so a realistic diagram could be drawn.

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
The vertices of triangle ABC are A(11,3), B(2k, k) and C(-1,-11).
(a) Find the two possible values of k if angle ABC is 90°.
(b) Draw the diagrams to show the two possible triangles.
~~~~~~~~~~~~~~~~~~


How the problem is posed/worded/formulated in the post,
its educational meaning disappeared, in full.

Meanwhile, the meaning can be restored and problem can be nicely presented
as a nice problem, if to re-formulate it in a right way.

This right way to re-formulate is as follows: 

    The vertices of triangle ABC are A(11,3), B(2k, k) and C(-1,-11).
    How to construct geometrically the point B (two possible positions)
    in a way that the triangle ABC be a right-angled triangle with the right angle at B ?


Then the answer (the geometric construction) is as follows: 

    (a)  draw a circle with the diameter AC;

    (b)  then draw the straight line y = 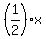%281%2F2%29x.

    (c)  Two intersection points of the line with the circle will give 
         two possible positions/locations of the vertex B.