Question 1195552: In 2010 Staci invested $14,000 in a savings account for her newborn son. The account pays 4.6% interest each year. Determine the accrued value of the account in the year 2028, when her son will go to college. Round your answer the nearest cent.
In the year 2028, the accrued value will be $
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
In 2028, 18 years after 2010, the accrued value of the account will be
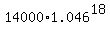 = 31,455.63 dollars. ANSWER
Solved.
----------------
For all details and explanations, look into these two lessons
- Compound interest percentage problems
- Problems on discretely compound accounts
in this site, and learn the subject from there.
After reading these lessons, you will tackle such problems on your own without asking for help from outside.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Happy learning (!)
Answer by math_tutor2020(3816)  (Show Source):
|
|
|
