Question 1195543: In 1990, the cost of tuition at a large Midwestern university was $102 per credit hour. In 1999, tuition had risen to $237 per credit hour.
Determine a linear function
C
(
x
)
to represent the cost of tuition as a function of
x
, the number of years since 1990.
C
(
x
)
=
In the year 2005, tuition will be $
per credit hour.
In the year
, tuition will be $357 per credit hour
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! straight line equation is y = mx + b
m is the slope
b is the y-intercept.
1990 is the base year.
that's when x = 0
1999 is 9 years after 1990.
that's when x = 9
the slope is equal to (y2 - y1) / (x2 - x1)
(x1,y1) = (0,102)
the value of y is 102 when the value os x = 0
(x2,y2) = (9,237)
the value of y is 237 when x = 9
the slope will be equal to (237 - 102) / (9 - 0) = 15.
the equation becomes y = 15 * x + 102
the equation tells you that the cost of tuition is growing at a linear rate of 15 dollars per year.
the year 2005 is 15 years after the year 1990.
the tuition will be equal to 15 * 15 + 102 = 327 in the year 2005.
to find when the tuition will be 357 dollars, replace y in the equation with t hat to get 357 = 15 * x + 102.
subtract 102 from both sides of the equation to get 255 = 15 * x
divide both sides of the equation by 15 to get 17 = x
when x = 17, the years is 1990 + 17 = 2007.
the equation can be graphed as shown below:
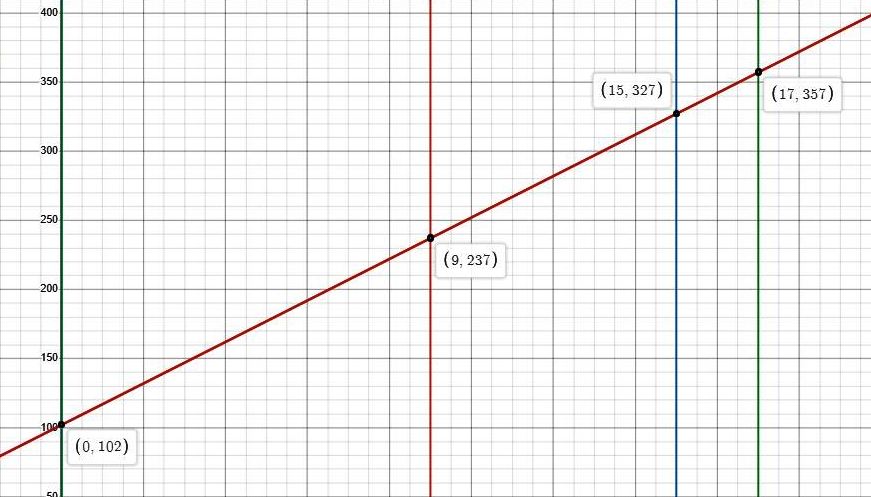
your solutions are:
the equation is y = 15 * x + 102 *****
in 1990, the tuition is 102 (given).
in 1999, the tuition is 237 (given).
in 2005, the tuition will be 15 * 15 + 102 = 327 *****
the tuition will be 357 in 2007 *****
here's a reference on straight line equations.
https://www.purplemath.com/modules/strtlneq.htm
let me know if you have any questions.
theo
|
|
|