Question 1194697: From a car traveling east at 40 mi.per hr., an airplane traveling horizontally
north at 100 mi.per hr, is visible 1 mi. east, 2 mi. south and 2 mi. up.
Find when the two will be nearest together.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From a car traveling east at 40 mi.per hr., an airplane traveling horizontally
north at 100 mi.per hr, is visible 1 mi. east, 2 mi. south and 2 mi. up.
Find when the two will be nearest together.
~~~~~~~~~~~~~~
We place the initial position of the car at the origin of the coordinate system (x,y,z) = (0,0,0).
Then the airplane's initial position is (x,y,z) = (1,-2,2).
The trajectory of the car in time is (40t,0,0).
The trajectory of the plane in time is (0,-2+100t,2).
The vector from the car to the airplane in the coordinate form is (-40t,-2+100t,2).
The square of the length of this vector (= the distance between the objects) is
d^2(t) = 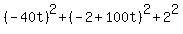 = = 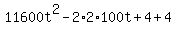 =
= =
= 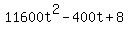 .
The distance d(t) is minimum when d^2(t) is minimum.
d^2(t) is minimum at t = " .
The distance d(t) is minimum when d^2(t) is minimum.
d^2(t) is minimum at t = "  " = - " = -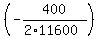 = 0.017241 of an hour = 1.0345 minutes.
At this time moment, the square of the distance is d^2(t) = = 0.017241 of an hour = 1.0345 minutes.
At this time moment, the square of the distance is d^2(t) = 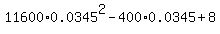 = 8.0069 mi^2,
hence, the distance itself is d(t) = = 8.0069 mi^2,
hence, the distance itself is d(t) = 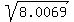 = 2.830 miles.
Compare it with the initial distance d(0) = = 2.830 miles.
Compare it with the initial distance d(0) = 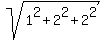 = =  = 3 miles. = 3 miles.
Solved.
------------------
On finding minimum of a quadratic function, see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
|
|
|