Question 1186415: f(x) = x^3 - 2 and g(x) = x^2 - 5x. Solve gf(x) = 6
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The polynomial equation gf(x) = 6, written exactly as presented in this post, has the form
(x^2-5x)*(x^3-2) = 6
which is the same as
x^5 - 5x^3 - 2x^2 + 4 = 0 (after FOIL and combining like terms).
As an authoritative online calculator
https://www.mathportal.org/calculators/solving-equations/polynomial-equation-solver.php
says, this equation HAS NO rational roots that can be found using Rational Root Theorem.
They only can be found using numerical methods.
Approximate values are
x1 = 0.84379
x2 = −2.1159
x3 = 2.35435
x4 = −0.54112 + 0.81167*i
x5 = −0.54112 − 0.81167*i
From the other side, if to suppose that the correct form of the given equation is different, namely, is
gof(x) = 0 (1) (composition of polynomial functions instead of their product),
then the EXACT solution can be obtained ANALYTICALLY.
This analytic solution is presented in other my post at this forum, where I solved this problem couples of days ago. See the link
https://www.algebra.com/algebra/homework/playground/test.faq.question.1186259.html
For your convenience, I copy/paste this solution here AGAIN.
/////////////////////
Introduce new variable y = x^3 - 2.
Then the given equation (1) takes the form
y^2 - 5y = 6
or
y^2 - 5y - 6 = 0.
Factor left side
(y-6)*(y+1) = 0,
which gives the roots y= 6 and y= -1.
If y= 6, then x^3 - 2 = 6, x^3 = 6 + 2 = 8, which implies x = 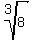 = 2.
If y= -1, then x^3 - 2 = -1, x^3 = -1 + 2 = 1, which implies x = = 2.
If y= -1, then x^3 - 2 = -1, x^3 = -1 + 2 = 1, which implies x =  = 1.
So, the real roots of the equation (1) are the values 1 and/or 2.
If you want to get all complex roots of equation (1), you should obtain complex roots of equations
x^3 = 8 and x^3 = 1.
They are x = = 1.
So, the real roots of the equation (1) are the values 1 and/or 2.
If you want to get all complex roots of equation (1), you should obtain complex roots of equations
x^3 = 8 and x^3 = 1.
They are x = 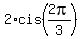 and and  for equation x^3 = 8, and x = for equation x^3 = 8, and x = 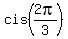 and and  for equation x^3 = 1.
Thus the full list of the solutions to equation (1) is
1, for equation x^3 = 1.
Thus the full list of the solutions to equation (1) is
1, 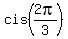 , ,  , 2, , 2, 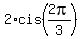 and and  . .
Solved.
|
|
|