Question 1185943: 1.the geometric mean between the first two terms is 32.if the third term is 4.find the first term
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
the geometric mean between the first two terms  is 32. is 32.
if the third term is 4, find the first term.
~~~~~~~~~~~~~~~~~~~~~~~~
@MathLover1 incorrectly read, interpret and treat the problem.
Her solution and her answer are incorrect.
I came to bring a correct solution.
The three terms of the geometric progression are a, ar, ar^2, from the first term to the third, inclusive.
Since the problem talks about "geometric mean", it means that the first two terms are POSITIVE,
and HENCE, all the terms of this GP are positive; in particular, "a" is positive and "r" is positive.
The geometric men of the first two terms is
GM(a,ar) = 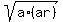 = = 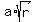 .
So, the first equation is .
So, the first equation is
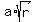 = 32. (1)
The second equation is = 32. (1)
The second equation is
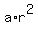 = 4. (2)
Dividing equation (2) by equation (1), you get
r^(3/2) = = 4. (2)
Dividing equation (2) by equation (1), you get
r^(3/2) = 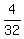 = =  = = 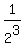 .
Hence, r^(1/2) = .
Hence, r^(1/2) =  and r = and r =  .
THEREFORE, the first term is .
THEREFORE, the first term is 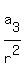 = = 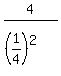 = = 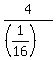 = 4*16 = 64.
ANSWER. The first term of the geometric progression is 64.
CHECK. Then the terms of the progression are 64, = 4*16 = 64.
ANSWER. The first term of the geometric progression is 64.
CHECK. Then the terms of the progression are 64, 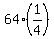 = 16, = 16, 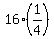 = 4,
and the geometric mean of the first two terms is = 4,
and the geometric mean of the first two terms is 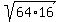 = = 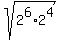 = = 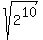 = =  = 32. ! Correct ! = 32. ! Correct !
Solved (correctly).
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|