SOLUTION: A 2 kg block is pulled with uniform speed up a plane which makes 30 degrees with the horizontal by a force of 15 N which is parallel to the plane. Find the coefficient of kinetic f

Algebra ->  Test -> SOLUTION: A 2 kg block is pulled with uniform speed up a plane which makes 30 degrees with the horizontal by a force of 15 N which is parallel to the plane. Find the coefficient of kinetic f      Log On


   

Question 1182826: A 2 kg block is pulled with uniform speed up a plane which makes 30 degrees with the horizontal by a force of 15 N which is parallel to the plane. Find the coefficient of kinetic friction between the block and the plane.
Answer by ikleyn(52777) About Me  (Show Source):
You can put this solution on YOUR website!
.
A 2 kg block is pulled with uniform speed up a plane which makes 30 degrees with the horizontal by a force of 15 N
which is parallel to the plane. Find the coefficient of kinetic friction between the block and the plane.
~~~~~~~~~~~~~ 


Since the block is pulled uniformly up the plane, it means that the force of 15 N parallel to the plane
is equal to the sum of the rolling force and the friction force.


The rolling force  R  parallel to the inclined plane is  R = m*g*sin(30°) = 2*10*(1/2) = 10 newtons.


The normal reaction force N, which is PERPENDICULAR to the inclined plane, has the value of  


    N = m*g*cos(30°) = 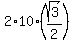2%2A10%2A%28sqrt%283%29%2F2%29 = 10%2Asqrt%283%29 = 17.32 newtons.


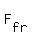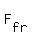The friction force  F%5Bfr%5D  is equal to  F%5Bfr%5D = k*N = 17.32*k,  where "k" is the kinematic friction coefficient.


So we have this equation to find out the kinetic friction coefficient


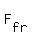    15 = R + F%5Bfr%5D = 10 + 17.32k.


From the equation, we find


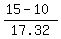    k = %2815-10%29%2F17.32 = 0.287   (the dimensionless value).


ANSWER.  Under given condition, the kinetic friction coefficient value is  0.287.

Solved.