Question 1182784: The coefficient of static friction between a 20-kg block and a horizontal surface is 0.25 and the coefficient of kinetic friction is 0.15. A cord is attached to the block, the cord making an angle of 10 degrees with the horizontal. (a) What tension in the cord will just start the block? (b) What is the tension in the cord when the block moves with uniform velocity?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The coefficient of static friction between a 20-kg block and a horizontal surface is 0.25
and the coefficient of kinetic friction is 0.15. A cord is attached to the block,
the cord making an angle of 10 degrees with the horizontal.
(a) What tension in the cord will just start the block?
(b) What is the tension in the cord when the block moves with uniform velocity?
~~~~~~~~~~~~~~~
The plot to the problem is shown in the Figure below.
 Figure. The body on the horizontal floor
Decompose the given force F into horizontal Fx and vertical Fy components.
Horizontal component Fx is equal to F*cos(10°); vertical component Fy is F*sin(10°).
The reaction force N acts from the floor vertically up to the box. Together with
vertical component Fy it balances the weight: W = Fy + N. So, N = W - Fy = mg - Fy.
The condition of start moving is that the horizontal force component Fx is equal
to the reaction force multiplied by the static friction coefficient
Fx =
Figure. The body on the horizontal floor
Decompose the given force F into horizontal Fx and vertical Fy components.
Horizontal component Fx is equal to F*cos(10°); vertical component Fy is F*sin(10°).
The reaction force N acts from the floor vertically up to the box. Together with
vertical component Fy it balances the weight: W = Fy + N. So, N = W - Fy = mg - Fy.
The condition of start moving is that the horizontal force component Fx is equal
to the reaction force multiplied by the static friction coefficient
Fx = 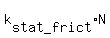 , or F*cos(10°) = 0.25*(mg - F*sin(10°)).
From the last equation, F*cos(10°) + 0.25*F*sin(10°) = 0.25*mg, which gives for the magnitude of F
F = , or F*cos(10°) = 0.25*(mg - F*sin(10°)).
From the last equation, F*cos(10°) + 0.25*F*sin(10°) = 0.25*mg, which gives for the magnitude of F
F = 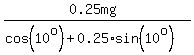 = =  = 48.614 N.
So, the tension of the cord, the force F, to start moving is 48.614 newtons.
It is the answer to question (a).
The condition of moving with the constant velocity is that the horizontal force component Fx is equal
to the reaction force multiplied by the kinetic friction coefficient
Fx = = 48.614 N.
So, the tension of the cord, the force F, to start moving is 48.614 newtons.
It is the answer to question (a).
The condition of moving with the constant velocity is that the horizontal force component Fx is equal
to the reaction force multiplied by the kinetic friction coefficient
Fx = 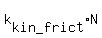 , or F*cos(10°) = 0.15*(mg - F*sin(10°)).
From the last equation, F*cos(10°) + 0.15*F*sin(10°) = 0.15*mg, which gives for the magnitude of F
F = , or F*cos(10°) = 0.15*(mg - F*sin(10°)).
From the last equation, F*cos(10°) + 0.15*F*sin(10°) = 0.15*mg, which gives for the magnitude of F
F = 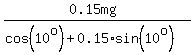 = = 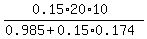 = 29.67 N.
So, the tension of the cord, the force F, to move the block uniformly is 29.67 newtons.
It is the answer to question (b). = 29.67 N.
So, the tension of the cord, the force F, to move the block uniformly is 29.67 newtons.
It is the answer to question (b).
Solved.
------------
In this solution, I used the approximate value of 10 m/s^2 for the gravity acceleration
instead of the more precise value of 9.81 m/s^2.
|
|
|