.
Joe Nedney of the San Francisco 49ers kicked a field goal with an initial velocity of 20m/s at an angle of 60∘.
a. How long is the ball in the air? Hint: you may assume that the ball lands at the same
height as it starts at.
b. What is the distance traveled by the ball before it hits the ground?
c. What is its maximum height?
~~~~~~~~~~~~~~~~~
(a) Vertical component of the initial velocity is 20*sin(60°) =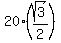 
= 17.32 ft/s.
Therefore, the equation for the verical coordinate h(t) is
h(t) = -16t^2 + 17.32t
The equation to find the time of the flight is h(t) = 0, or
-16t^2 + 17.32t = 0, or
t*(16t - 17.32) = 0
We are interested in positive root, ONLY, and this root is
t = 
= 1.0825 seconds. ANSWEER
(b) The horizontal component of the speed is 20*cos(60°) = 
= 10 ft/s and is considered as a constant during the flight.
Moving with the horizontal speed of 10 ft/s during 1.0825 seconds, the ball will get the ground at the distance of
1.0825*10 = 10.825 feet horizontally from starting position. ANSWER
(c) To find maximum height, notice that the time moving up is HALF of the total flight time, i.e., 
= 0.54125 seconds.
To find 
, calculate the function h(t) at t = 0.54125:
= -16*0.54125 + 17.32*0.54125 = 4.687 ft. ANSWER
Solved. // All questions are answered.
