SOLUTION: The value,$V, of a house n years after it was built is given by the formula V = 250000e^an. When n = 3, V = 350 000. Finde the initial value of this house. Find the value of a. Est

Algebra ->  Test -> SOLUTION: The value,$V, of a house n years after it was built is given by the formula V = 250000e^an. When n = 3, V = 350 000. Finde the initial value of this house. Find the value of a. Est      Log On


   

Question 1179585: The value,$V, of a house n years after it was built is given by the formula V = 250000e^an. When n = 3, V = 350 000. Finde the initial value of this house. Find the value of a. Estimate the number of years for this house to double in value.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

V+=+250000e%5E%28an%29
When n+=+3, V+=+350000
Finde the initial value of this house. Find the value of a.
350000=+250000e%5E%28a%2A3%29
350000%2F250000=e%5E%28a%2A3%29
7%2F5=e%5E%28a%2A3%29............take ln of both sides
ln%287%2F5%29=ln%28e%5E%28a%2A3%29%29
ln%287%2F5%29=%28a%2A3%29ln%28e%29
3a=ln%287%2F5%29%2Fln%28e%29..............ln(e)=1
3a=ln%287%2F5%29
a=%28ln%287%29-ln%285%29%29%2F3
a=0.1122
Estimate the number of years for this house to double in value.
2%2A350000=+250000e%5E%280.1122%2An%29
700000%2F250000=e%5E%280.1122%2An%29
14%2F5=e%5E%280.1122%2An%29 ...........take ln of both sides
ln%2814%2F5%29=ln%28e%5E%280.1122%2An%29%29
ln%2814%29-ln%285%29=%280.1122%2An%29ln%28e%29
ln%282%2A7%29-ln%285%29=%280.1122%2An%29%2A1
ln%282%29%2Bln%287%29-ln%285%29=0.1122%2An
1.0296194171811581=0.1122%2An
n=1.0296194171811581%2F0.1122
n=9.18
this house will double in value in 9.18 years

Answer by ikleyn(52777) About Me  (Show Source):
You can put this solution on YOUR website!
.
The value,$V, of a house n years after it was built is given by the formula V = 250000e^an. When n = 3, V = 350 000.
(a) Find the initial value of this house.
(b) Find the value of a.
(c) Estimate the number of years for this house to double in value.
~~~~~~~~~~~~ 


(a)  The initial value of this house is  250,000  (it is the value provided by the formula at n = 0).

     It is the ANSWER for the part (a).



(b)  Find the value of "a" from this equation  (the value in 3 years)

         350000 = 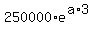250000%2Ae%5E%28a%2A3%29


     Divide both sides by 25000

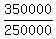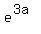         350000%2F250000%29 = e%5E%283a%29

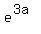         1.4 = e%5E%283a%29


     Take natural logarith (base e) of both sides

         ln(1.4) = 3a*ln(e) = 3a

         a = ln%281.4%29%2F3 = 0.112157.   


      It is the ANSWER  for the part (b).


         +--------------------------------------------------------------+
         |   I made this solution and these computations to show you    |
         |   HOW SIMPLE they are.                                       |
         |                                                              |
         |   You do not need make the tons of unnecessary calculations  | 
         |   that @MathLover1 does.                                     |
         +--------------------------------------------------------------+



(c)  When they ask you to estimate the number of years for this house to double its value,

     then FOR SURE whey consider the doubling of the INITIAL value, if the opposite is not stated explicitly.


     So, your equation to find "n" is THIS

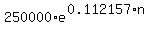         500000 = 250000%2Ae%5E%280.112157%2An%29.


     Notice that I used the value of "a"  0.112157, which I found in part (b).


     In the equation, divide both sides by 250000 to get

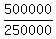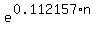         500000%2F250000 = e%5E%280.112157%2An%29

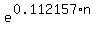               2 = e%5E%280.112157%2An%29


     Take natural logarith base e of both sides

              ln(2) = 0.112157*n

     and find "n"

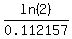               n = ln%282%29%2F0.112157 = 6.18 years.


     It is the ANSWER to part (c).

Solved.

-------------------

From my post,  learn how to solve the problem in the shortest way,  without making unnecessary calculations.

Also,  note that the answer by  @MathLover1  to part  (c) is  IRRELEVANT.