Question 116625: Solve this equation.
5^x^3 = 25^x
x =________________(smallest value)
x =
x =__________________(largest value
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! In case you can still use an answer to this problem, here's how you can do it.
.
The biggest lesson that you can learn from this problem is that anytime you see a variable used
as an exponent, you should think of the possibility of using logarithms to solve the problem
because if you take the logarithm of such a quantity, the exponent can be brought out as the
multiplier of the logarithm. This is true regardless of base in the logarithm. For example:
.
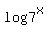 is equal to is equal to 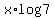
.
In this problem you are given the equation:
.

.
If you take the Logarithm of both sides (any base will do, but just for simplicity let's
use base 10), the equation becomes:
.

.
bringing out the exponents and making them multipliers converts the problem to:
.

.
But notice on the right side that 25 can be replaced by  making the equation become: making the equation become:
.

.
Applying the exponent property again on the right side, the 2 comes out as a multiplier and
you have:
.

.
Notice now that 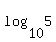 is a factor of both sides, and it is just a number that you is a factor of both sides, and it is just a number that you
can get using a calculator. [Should you be interested, that number is 0.698970004].
If both sides of the equation are divided by 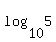 the logarithmic term just the logarithmic term just
cancels on both sides and the equation is reduced to:
.

.
Get rid of the 2x on the right side by subtracting 2x from both sides to get:
.

.
Factor the left side and you get:
.

.
This equation will be true if either of the factors on the left side equals zero because then
the left side would involve a multiplication by zero and that zero multiplier would make
the entire left side equal to zero ... therefore equaling the right side.
.
So setting the first factor equal to zero just gives:
.

.
Then setting the second factor equal to zero gives:
.

.
Add 2 to both sides and you get:
.

.
Solve for x by taking the square root of both sides and you have:
.
 and and 
.
In summary, the three answers to this problem are:
.



.
If you substitute each of these three values back into the original equation, you will find
that the equation is true.
.
For example: Start with the original equation:
.

.
Substitute 0 for x and you have:
.

.
but you know that that when any quantity is raised to the zero power the answer is 1. So this
equation reduces to:
.

.
And this is obviously true ... so x = 0 is a good solution.
.
Next start with the original equation and substitute  for x. for x.
.
The original equation is:
.

.
Substitute 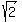 for x and get: for x and get:
.

.
On the right side replace 25 with  and the equation becomes: and the equation becomes:
.

.
On the left side cubing  is equivalent to is equivalent to 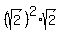 and and 
so cubing  results in results in  . This makes the equation become: . This makes the equation become:
.

.
Finally on the right side, the power rule of exponents tells you to multiply 2 times 
and this makes the equation become:
.

.
Note that the left side now equals the right side, so  is a good solution is a good solution
to the problem.
.
You can do the proof for  . It works very similar to the one for . It works very similar to the one for  . .
.
I know this is late, but the lessons involved in solving this problem are hopefully in
time to help you understand the concepts involved in getting a solution.
.
Happy holidays to you and yours ...
|
|
|