Question 1164851: What must be done to a function's equation so that its graph is shifted vertically upward? Compare this to what must be done so that its graph is shifted horizontally to the right.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! to shift the graph vertically upward, you need add a constant to the end of it.
so, if your equation is f(x), then your new equation has to be f(x) + a, where is a positive constant.
to shift the graph horizontally to the right, you need to subtract a constant from the variable used.
so, if your equation is f(x), then your new equation has to be f(x-a), where a is a positive constant.
for example:
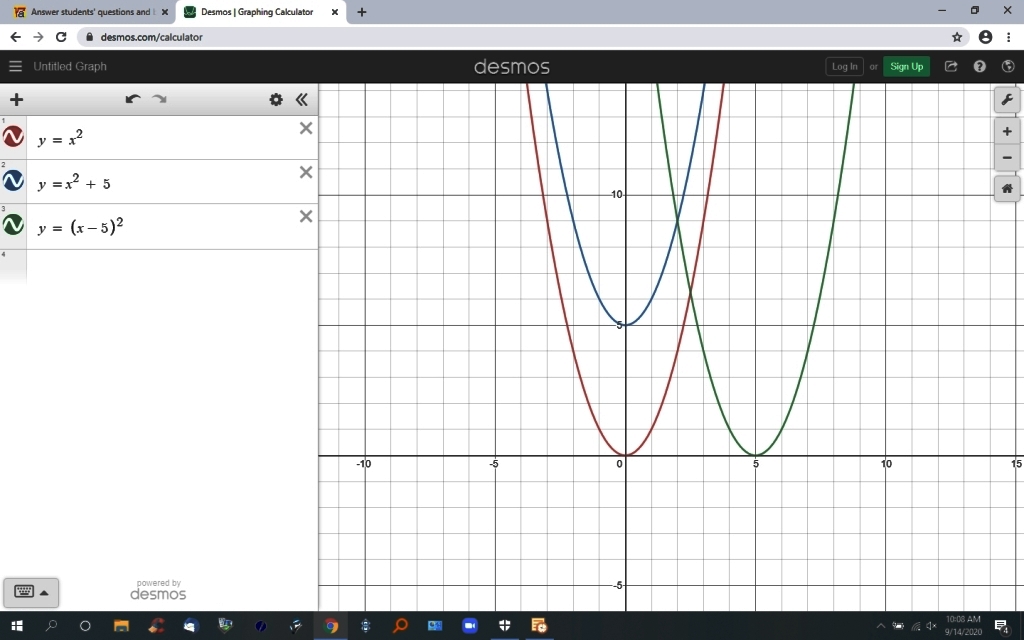
consider the equation of f(x) = x^2
f(x) + 5 = x^2 + 5 shifts the equation up 5 units.
this means that the value of y for the same value of x is 5 units more positive than the original equation.
you can see on the graph, that, in the equation of y = x^2, y = 0 when x = 0.
you can also see on the graph, that, in the equation of y = x^2 + 5, y = 5 when x = 0.
in the graph, y = x^2 is red and y = x^2 + 5 is blue.
now consider the equation of f(x) = x^2 again.
f(x-5) = (x-5)^2 shift the equation to the right 5 units.
this means that the value of x for the same value of y is 5 units to the right of the original equation.
you can see on the graph that, in the equation of y = x^2, x = 0 when y = 0.
you can also see on the graph that, in the equation of y = (x-5)^2, x = 5 when y = 0.
in the graph, y = x^2 is red and y = (x-5)^2 is green.
here's the graph.
note that the use of f(x) and the use of y is interchangeable.
that's because f(x) = y.
you can say y = x^2 and you can say f(x) = x^2 and it means the same thing.
|
|
|