.
There are 50 iPads available for check. Of them, 10 are defective.
A sample of 3 iPads is randomly selected without replacement.
What is the probability that at least one of the iPads is defective?
round to the nearest thousand
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I edited the original text to make it grammatically correct.
Also, I removed all the words that are irrelevant, to transform
from the " bla-bla-bla " style to normal mathematical style.
- - - - - - - - S o l u t i o n 1 - - - - - - - -
An event "At least one is defective" is the complement to the event "No one is defective".
An event "No one is defective" means that our 3 randomly selected iPads are from the set
of 50-10 = 40 good iPads.
So, we write
P(at least one is defective = 1 - P(no one is defective) = 1 -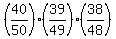 
= 0.496 (rounded).
At this point, the solution 1 is complete. The answer is P = 0.496 (rounded).
- - - - - - - - S o l u t i o n 2 - - - - - - - -
An event "At least one is defective" is the complement to the event "No one is defective".
An event "No one is defective" means that our 3 randomly selected iPads are from the set
of 50-10 = 40 good iPads.
So, we write
P(at least one is defective = 1 - P(no one is defective) = 1 -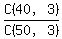 
= 1 - 
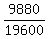= 0.496 (rounded).
Here we relate C(40,3) = 9880 triples (combinations), consisting of good iPads only,
to C(50,3) = 19600, the number of all possible triples (combinations).
At this point, the solution 2 is complete. The answer is the same: P = 0.496 (rounded).
Solved completely in two different ways for your better understanding.
