Question 1156758: Suppose an airline policy states that all baggage must be boxshaped with a sum of length, width, and height not exceeding 168in. What are the dimensions and
volume of a squarebased box with the greatest volume under these conditions?
Write a function for the volume V of the box in terms of w, one of the edges of
the square bottom.
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Suppose an airline policy states that all baggage must be boxshaped with a sum of length, width, and height not exceeding 168in.
What are the dimensions and
volume of a squarebased box with the greatest volume under these conditions?
Greatest volume would be a cube
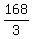 = 56 by 56 by 56 which is 56^3 = 175,616 cu inches
:
Write a function for the volume V of the box in terms of w, one of the edges of
the square bottom.
w = one side of the square bottom
sum of the length, width and height = 168, the bottom is square, therefore:
h = (168-2w)
V = w^2 * h
replace h with (168-2w)
V = w^2 * (168-2w)
V = -2w^3 + 168w^2
|
|
|
