SOLUTION: [3 + 2√(2)]ⁿ + [3 - 2√(2)]ⁿ = 34

Algebra ->  Test -> SOLUTION: [3 + 2√(2)]ⁿ + [3 - 2√(2)]ⁿ = 34      Log On


   

Question 1155666: [3 + 2√(2)]ⁿ + [3 - 2√(2)]ⁿ = 34
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

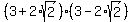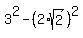Notice that %283%2B2%2Asqrt%282%29%29%2A%283-2%2Asqrt%282%29%29 = 3%5E2+-+%282%2Asqrt%282%29%29%5E2 = 9 - 8 = 1.


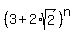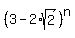So, if we introduce new variables  x = %283%2B2%2Asqrt%282%29%29%5En  and  y = %283-2%2Asqrt%282%29%29%5En, then we have this system of 2 equations in 2 unknowns


    x + y = 34

    xy    = 1


It leads to the equation in one unknown

    x + 1%2Fx = 34

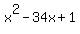    x%5E2+-+34x+%2B+1 = 0

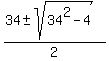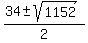    x%5B1%2C2%5D = %2834+%2B-+sqrt%2834%5E2-4%29%29%2F2 = %2834+%2B-+sqrt%281152%29%29%2F2


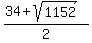So,  x%5B1%5D = %2834+%2B+sqrt%281152%29%29%2F2 = 33.97056,

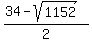     x%5B2%5D = %2834+-+sqrt%281152%29%29%2F2 = 0.029437.


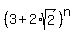Therefore,  if x = 33.97056, then  %283%2B2%2Asqrt%282%29%29%5En = 33.97056;  hence  n = 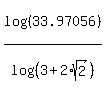log%28%2833.97056%29%29%2Flog%28%283%2B2%2Asqrt%282%29%29%29 = 2.


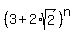            if x = 0.029434, then  %283%2B2%2Asqrt%282%29%29%5En = 0.029434;  hence  n = log%28%280.029434%29%29%2Flog%28%283%2B2%2Asqrt%282%29%29%29 = -2.


CHECK.  I will check for n = 2 only.


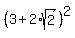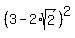        %283+%2B+2%2Asqrt%282%29%29%5E2 + %283+-+2%2Asqrt%282%29%29%5E2 = 3^2 + 8 + 3^2 + 8 = 18 + 16 = 34.   ! Precisely correct !


ANSWER.  n = 2 and/or -2.