Question 1155423: Find the critical points of the following function.
f(x)=x^2sqrt(x+14)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose that x=c is a critical point of 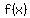 . .
If  ' '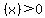 to the left of to the left of  and and  ' '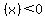 to the right of to the right of  , then , then  is a local maximum. is a local maximum.
If  ' '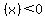 to the left of to the left of  and and  ' '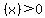 to the right of to the right of  , then , then  is a local minimum. is a local minimum.
If  ' ' is the same sign on both sides of is the same sign on both sides of  then then  is neither a local maximum nor a local minimum. is neither a local maximum nor a local minimum.
 .....derivate .....derivate
apply the Product Rule:  '= '= '* '*  + + * * ' '






equate to zero and solve for 
 -> will be zero if -> will be zero if



 -> complex solution, derivative is undefined -> complex solution, derivative is undefined
if 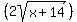 derivative is undefined derivative is undefined
Critical points are points where the function is defined and its derivative is zero or undefined
 , ,  , ,  -> a critical points -> a critical points
Identify critical points not in f (x ) domain :  is [ is [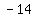 ) )



maximum is at: ( , , ) )




minimum is at: ( , , ) )


minimum is at: ( , , ) and ( ) and ( , , ) )
maximum is at (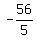 , , ) )
 is monotone in intervals: is monotone in intervals:
( , ,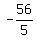 ) -> ) ->  is increasing is increasing
(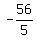 , , )-> )-> is decreasing is decreasing
|
|
|