Question 1153562: The number n - 4, n + 2, 3n + 1 are in geometrical progression. Find the two possible values of the common ratio.
Found 3 solutions by MathLover1, ikleyn, MathTherapy:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The number n - 4, n + 2, 3n + 1 are in  geometric progression. geometric progression.
Find the two possible values of the common ratio.
~~~~~~~~~~~~~~~~~~~
Notice that THERE IS NO SUCH a term "geometrical progression" in Math.
There is the term "geometric progression", instead.
Since the three numbers are in geometric progression, we have this equality
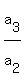 = =  , (1) or , (1) or
 = = 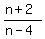 . (2)
They assume you will find the value "n" from this equation and then evaluate the common ratio.
To find "n", cross multiply equation (2)
(3n+1)*(n-4) = . (2)
They assume you will find the value "n" from this equation and then evaluate the common ratio.
To find "n", cross multiply equation (2)
(3n+1)*(n-4) = 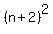 3n^2 - 12n + n - 4 = n^2 + 4n + 4
2n^2 - 15n - 8 = 0
3n^2 - 12n + n - 4 = n^2 + 4n + 4
2n^2 - 15n - 8 = 0
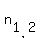 = = 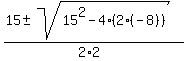 = = 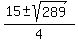 = = 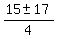 .
One root is .
One root is 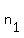 = = 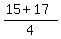 = = 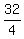 = 8.
With this value of n, the common ratio of the GP is = 8.
With this value of n, the common ratio of the GP is
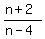 = = 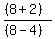 = =  = =  = 2.5.
The other root is = 2.5.
The other root is 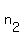 = = 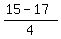 = =  .
With this value of n, the common ratio of the GP is .
With this value of n, the common ratio of the GP is
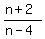 = = 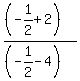 = = 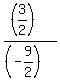 = =  .
ANSWER. Two possible values of the common ratio are .
ANSWER. Two possible values of the common ratio are  and and  . .
Solved and answered.
--------------------
There is a bunch of lessons on geometric progressions in this site
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Solved problems on geometric progressions
- Word problems on geometric progressions
- One characteristic property of geometric progressions
- Fresh, sweet and crispy problem on arithmetic and geometric progressions
- Mathematical induction and geometric progressions
- Mathematical induction for sequences other than arithmetic or geometric
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Geometric progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The number n - 4, n + 2, 3n + 1 are in geometrical progression. Find the two possible values of the common ratio.
Correct answer: 
|
|
|