SOLUTION: Find the difference between the sums of the first ten terms of the Geometrical and Arithmetical Progressions which begin with 6 + 12 + ...

Algebra ->  Test -> SOLUTION: Find the difference between the sums of the first ten terms of the Geometrical and Arithmetical Progressions which begin with 6 + 12 + ...       Log On


   

Question 1153524: Find the difference between the sums of the first ten terms of the Geometrical and Arithmetical Progressions which begin with 6 + 12 + ...
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 6, 12, ... is a geometric progression with common ratio r=2
6=3%2A2%5E1
12=3%2A2%5E2
general: 3%2Ar%5En
first 10 terms are:+6,12,24,48,96,192,384,768,1536,3072
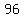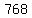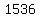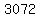
the sum is: 6%2B12%2B24%2B48%2B96%2B192%2B384%2B768%2B1536%2B3072=6138
and
an arithmetic progression (AP), also called an arithmetic sequence, is a sequence of numbers which differ from each other by a common difference. For example, the sequence +6,12, is an arithmetic sequence with the common difference d=6.
general: a%5Bn%5D=a%5Bn-1%5D%2Bd
first 10 terms are: 6,12,18,24,30,36,42,48,54,60+
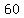
the sum is: 6%2B12%2B18%2B24%2B30%2B36%2B42%2B48%2B54%2B60=+330

Answer by MathTherapy(10549) About Me  (Show Source):
You can put this solution on YOUR website!

Find the difference between the sums of the first ten terms of the Geometrical and Arithmetical Progressions which begin with 6 + 12 + ... 
Larger of the 2 is the GP: 

Smaller of the 2 is the AP: 

Difference between the 2 sums of the 1st 10 terms: