Question 1152686: Two lines L1 and L2 intersect at point P.L1 passes through points(-4,0)and(0,6).
Given that L2 has the equation:y=2x-2,find by calculation the coordinates of P.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! line 1 passes through the points (-4,0) and (0,6)
let y1 = (-4,0) and let y2 = (0,6)
the slope of line 1 is (y2 - y1) / (x2 - x1) = 6/4 = 1.5.
the slope intercept format of a straight line is y = mx + b
m = the slope
b equal the y-intercept.
the y-intercept of line 1 is the value of y when x = 0.
that makes the y-intercept of line 1 equal to 6.
the equation of line 1 is therefore y = 1.5 * x + 6
the equation of line 2 is y = 2 * x - 2.
the two lines intersect when 1.5 * x + 6 = 2 * x - 2
subtract 1.5 * x from both sides of that equation and add 2 to both sides of that equation to get:
8 = .5 * x
solve for x to get:
x = 8 / .5 = 16
when x = 16, y = 1.5 * x + 6 becomes 30
when x = 16, y = 2 * x - 2 becomes 30
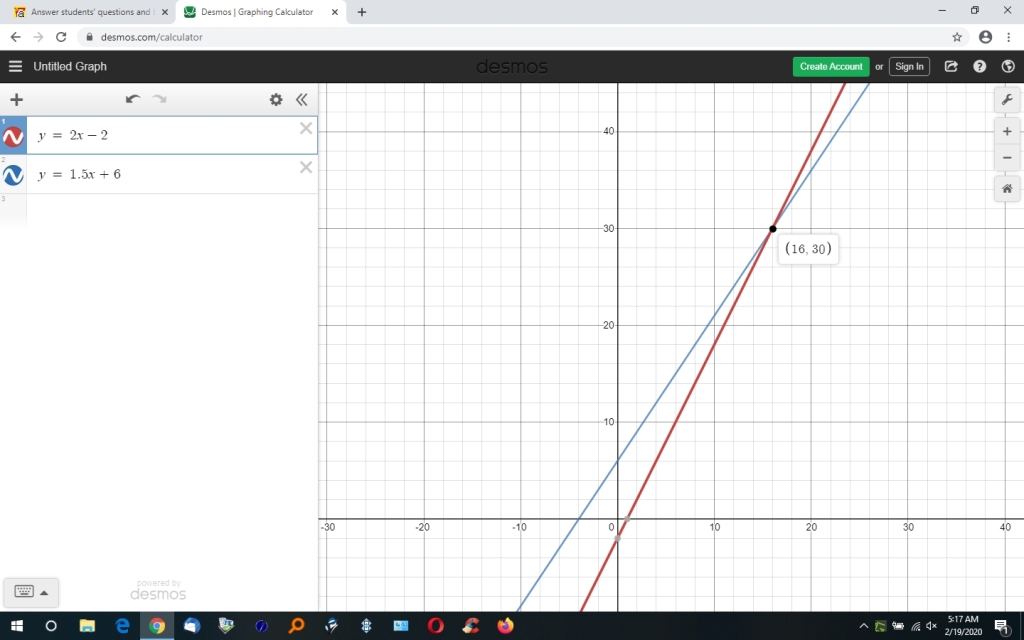
the point (16,30) is a common point to both lines and is therefore the intersection of those two lines.
here's what the graph of both those equations looks like.
it can be seen that the intersection of the two lines is at the point (16,30).
|
|
|