Question 1145006: If a, b, c are the zeroes of the polynomials p(x) = x³ + 4, then find the value of
k = - 3[(1/(a² - a + 1) + (1/(b² - b + 1)] + c
Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Surely and certainly, this problem is advanced and is intended for advanced students.
So, I will assume that your level corresponds to the problem's level.
(1) 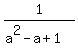 = = 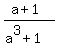 .
It follows from the standard identity .
It follows from the standard identity 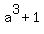 = = 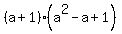 .
Further, since "a" is the root of the equation .
Further, since "a" is the root of the equation  = 0, we have = 0, we have
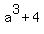 = 0; hence, = 0; hence, 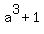 = = 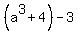 = =  = -3.
Therefore, = -3.
Therefore, 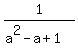 = = 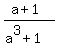 = = 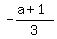 . (1)
(2) Similarly, . (1)
(2) Similarly, 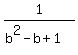 = =  . (2)
(3) Therefore,
k = - 3[(1/(a² - a + 1) + (1/(b² - b + 1)] + c = -3*( . (2)
(3) Therefore,
k = - 3[(1/(a² - a + 1) + (1/(b² - b + 1)] + c = -3*( 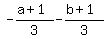 ) + c = (a+1) + (b+1) + c = (a + b + c) + 2.
The sum (a + b + c) is the coefficient of the given polynomial p(x) = x^3 + 4 at "x"; so, it is 0 (zero, ZERO) :
a + b + c = 0.
Therefore, k = 0 + 2 = 2. ANSWER
ANSWER. k = 2. ) + c = (a+1) + (b+1) + c = (a + b + c) + 2.
The sum (a + b + c) is the coefficient of the given polynomial p(x) = x^3 + 4 at "x"; so, it is 0 (zero, ZERO) :
a + b + c = 0.
Therefore, k = 0 + 2 = 2. ANSWER
ANSWER. k = 2.
********************
* * * S O L V E D * * *
********************
It is how the given problem is assumed to be solved and how it should be solved.
|
|
|