Question 1144754: Find x,
4^(x+1.5) + 9^(x+0.5) = 10×6^x
Found 3 solutions by greenestamps, ikleyn, Alan3354:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation has two terms on the left with different exponents involving the variable; the expression on the right has the variable in an exponent. Such equations can't be solved algebraically; numerical methods are needed.
Use a graphing calculator to find the answer.
The expressions on the two sides of the equation have values that are very nearly equal across a large part of the domain, so graphing the two expressions to find their intersection doesn't work well. Instead, graph the expression
4^(x+1.5) + 9^(x+0.5) - 10×6^x
and find where the value is 0.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is an advanced level exponential equation.
Nevertheless, it is SOLVABLE (!), and I will show you how.
4^(x+1.5) + 9^(x+0.5) = 10×6^x (1)
It is equivalent to
2^(2x+3) + 3^(2x+1) = 10*(2^x)*(3^x), or
8*2^(2x) + 3*3^(2x) = 10*(2^x)*(3^x). (2)
Introduce new variables u = 2^x, v = 3^x. Then equation (2) takes the form
8u^2 + 3v^2 = 10uv
Divide both sides by v^2. You will get
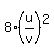 + 3 - + 3 - 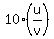 = 0 (3)
Let z = = 0 (3)
Let z = 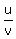 . Then equation (3) takes the form
8z^2 - 10z + 3 = 0.
Solve this quadratic equation using the quadratic formula . Then equation (3) takes the form
8z^2 - 10z + 3 = 0.
Solve this quadratic equation using the quadratic formula
 = = 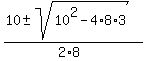 = = 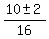 .
The roots are .
The roots are
 = = 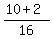 = = 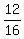 = =  , and , and
 = =  = = 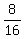 = =  .
Thus, we should consider two cases.
(a) .
Thus, we should consider two cases.
(a)  = =  .
It means .
It means  = = 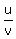 = = 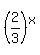 .
Next you can take any logarithm, log base 10, or natural logarithm "ln" to continue .
Next you can take any logarithm, log base 10, or natural logarithm "ln" to continue
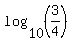 = = 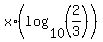 , ,
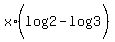 = = 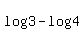 x =
x = 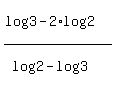 = = 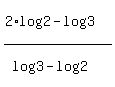 = 0.709511 (approximately).
The first case is completed.
Similarly, you can consider and complete the second case = 0.709511 (approximately).
The first case is completed.
Similarly, you can consider and complete the second case  = =  .
May I leave it to you, in order for you completed it on your own ? .
May I leave it to you, in order for you completed it on your own ?
If you still will have questions, let me know.
Come again to this forum soon to learn something new (!)
-----------------
As an accurate person, I checked my answer.
I used MS Excel in my computer and calculated the left side and the right side expressions of the original equation at x= 0.709511.
I got the value of 35.65389 on the left side and the value of 35.65389 on the right side.
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|