Question 1142422: If 4b² + 1/b² = 2, find 8b³ + 1/b³
Found 3 solutions by greenestamps, ikleyn, MathTherapy:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If 4b² + 1/b² = 2, find 8b³ + 1/b³
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by the other tutor has errors.
So I came to provide a correct solution.
You are given
 + + 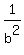 = 2. (1)
It is the same as = 2. (1)
It is the same as
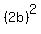 + + 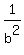 = 2.
Add 4 to both sides. You will get = 2.
Add 4 to both sides. You will get
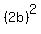 + 4 + + 4 +  = 6. (2)
The left side is nothing else as = 6. (2)
The left side is nothing else as 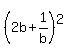 . Therefore, the equation (2) takes the form . Therefore, the equation (2) takes the form
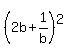 = 6.
Take the square root from both sides of the last equation. You will get = 6.
Take the square root from both sides of the last equation. You will get
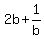 = +/- = +/-  . (3)
Now, . (3)
Now,
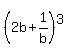 = = 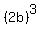 + + 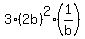 + + 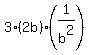 + + 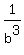 = = 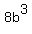 + + 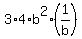 + + 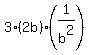 + + 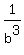 = = 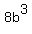 + + 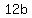 + +  + + 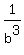 = = 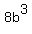 + + 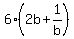 + + 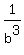 .
Thus the very first part of this chain of equalities is equal to its very last part .
Thus the very first part of this chain of equalities is equal to its very last part
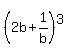 = = 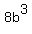 + + 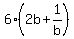 + + 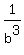 .
Hence, .
Hence,
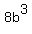 + + 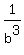 = = 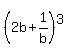 - - 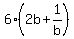 .
Now the final step is to substitute expression (3) into the last equality.
Since expression (3) has the sign +/-, I will make this substitution in two lines.
Case 1. If .
Now the final step is to substitute expression (3) into the last equality.
Since expression (3) has the sign +/-, I will make this substitution in two lines.
Case 1. If 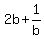 = + = +  , then , then 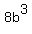 + + 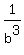 = = 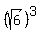 - -  = =  - -  = 0.
Case 2. If = 0.
Case 2. If 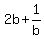 = - = -  , then , then 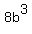 + + 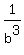 = = 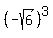 - - 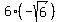 = = 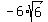 + +  = 0.
You see that for any of the two cases the answer is 0 (zero, ZERO).
ANSWER. If = 0.
You see that for any of the two cases the answer is 0 (zero, ZERO).
ANSWER. If  + + 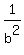 = 2, then = 2, then 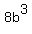 + + 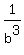 = 0. = 0.
---------------
This result seems to be VERY INEXPECTED, and you might be overwhelmed / stunned by this answer,
but the deep reason why it is so is that the given equation HAS NO real roots "b".
It has ONLY COMPLEX NUMBER solutions (!)
See the attached plot of the function y =  + + 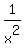 . .
 Plot y =
Plot y =  + + 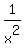 The plot shows that the function y =
The plot shows that the function y =  + + 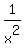 is always greater than 2, so the given equation has no real roots. is always greater than 2, so the given equation has no real roots.
--------------------
This problem is slightly ABOVE an averaged High school Math competition level, since it contains TWO UNDERWATER STONES
instead of standard ONE.
The second underwater stone is the complexity of the roots to the given equation, which makes it difficult to a student
to believe that the obtained result / (answer) is correct.
For the standard problems / (exercises) of the High school competition level, see the lessons
- HOW TO evaluate expressions involving  , , 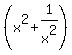 and and 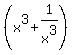
- Advanced lesson on evaluating expressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Evaluation, substitution".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|