SOLUTION: the width of a rectangle is 2 cm less than three times the length. The area is 96 square centimeters. Find the length and width of the rectangle. Sketch the rectangle.

Algebra ->  Test -> SOLUTION: the width of a rectangle is 2 cm less than three times the length. The area is 96 square centimeters. Find the length and width of the rectangle. Sketch the rectangle.      Log On


   

Question 1141264: the width of a rectangle is 2 cm less than three times the length. The area is 96 square centimeters. Find the length and width of the rectangle. Sketch the rectangle.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
x%283x-2%29=96
-
3x%5E2-2x-96=0

discrim, 4%2B4%2A3%2A96=1156=34%5E2

x=%282%2B-+34%29%2F6
needthepositivepart:


x=%2834%2B2%29%2F6

x=36%2F6=6

highlight%28x=6%29----------------width
-
3x-2=3%286%29-2=highlight%2816%29-------Length

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!
the width of a rectangle is 2 cm less than three times the length. The area is 96 square centimeters. Find the length and width of the rectangle. Sketch the rectangle.
Sketch it yourself!

Let length be L

Then width is: 3L - 2 

We then get the following AREA equation: L(3L - 2) = 96

You'll get a quadratic that CAN BE factored, or if you prefer, you can use the quadratic equation formula, complete the square or graph it to find L, and then W

BTW, the width is NOT cross%28highlight%28x=5%261%2F3%29%29, as the other person claims. 

The length, however has one of its values as 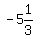-5%261%2F3, but is this possible? You figure it out!!