Question 1136573: Recursive equations can be very handy for modeling complicated situations for which explicit equations would be hard to interpret. As an example, consider a lake in which 2000 fish currently reside. The fish population grows by 10% each year, but every year 100 fish are harvested from the lake by people fishing.
a. Write a recursive equation for the number of fish in the lake after n years.
b. Calculate the population after 1 and 2 years. Does the population appear to be increasing or decreasing?
c. What is the maximum number of fish that could be harvested each year without causing the fish population to decrease in the long run?
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
I interpret this problem in this way:
Each year the fish population increase by 10%, but on tDecember, 31, each year a fisherman comes and harvests 100 fish at once.
Solution
(a)  =  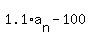,  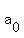= 2000, n = 1, 2, 3, . . .
(b)  = 1.1*2000 - 100 = 2100;
 = 1.1*2100 - 100 = 2210.
(c) This maximum value is exactly 10% of 2000, which is 200 fish.
Answered and solved.
-----------------
There is another area of human activity, where processes go precisely in accordance with this scheme.
It is withdrawing of certain amount of money at the end of each year from a banking account compounded annually.
This area is completely covered by mathematical formulas.
You can read about it and about adjacent issues from the lessons
- Ordinary Annuity saving plans and geometric progressions
- Annuity Due saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Withdrawing a certain amount of money periodically from a compounded saving account (*)
- Miscellaneous problems on retirement plans
in this site, and especially from the lesson marked (*) in the list as the most relevant to the given problem.
|
|
|
