SOLUTION: If d is the H.C.F of 45 and 27, find x, y satisfying d = 45x + 27y

H.C.F. is the Highest Common Factor and is the same as the Greatest Common Factor (GCF).


GCF of numbers 45 and 27 is 9, so the problem asks to find integers x and y satisfying

    9 = 45x + 27y.


Reducing by the factor 9 both sides, it is the same as to find integers x and y satisfying

    1 = 5x + 3y.


The solution is easy to find by the "trial and error method", and there is a nice method to automatize it using Excel.


You write y = 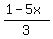,  give x the series of values 1, 2, 3, . . .  and look for x which gives integer value for y (see the Table below):


  T A B L E

x        y
-------------------

1	-1.333333333
2	-3
3	-4.666666667
4	-6.333333333
5	-8
6	-9.666666667
7	-11.33333333
8	-13


In our case, the second line of the Table just gives the solution  x= 2  and  y= -3.


Notice that after that, every third line of the Table gives the next solution.


So, the answer for the original problem are these two values  x= 2,  y= -3.