Question 1122273: At noon a culture of bacteria had 2.5x10^6 members, and at 3 pm the population was 4.5x10^6. Assuming exponential growth, find when the population will be 8.0x10^6.
Found 2 solutions by josgarithmetic, Theo:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you first need to find the exponential growth rate.
the formula for that is f = p * e^(rt)
f is equal to 4.5 * 10^6
p is equal to 1.5 * 10^6
t is equal to 3
you are solving for r.
formula becomes 4.5 * 10^6 = 1.5 * 10^6 * e^(3r)
divide both sides of this formula by 1.5 * 10^6 to get:
4.5 * 10^6 / (1.5 * 10^6) = e^(3r)
take the natural log of both sides of this formula and simplify to get:
ln(3) = ln(e^3r)
since ln(e^3r) is equal to 3r * ln(e) and ln(e) is equal to 1, this equation becomes:
ln(3) = 3r
solve for r to get:
r = ln(3) / 3
this results in r = .3662040962
that's your hourly exponential growth rate.
to see if this is good, take 1.5 * 10^6 and multiply it by e^(.3662040962 * 3).
you will get 4.5 * 10^6 which is exactly what you want, assuming the rate is calculated correctly, as it is.
to find out when the population will reach 8.0 * 10^6, use the same formula of f = p * e^(rt).
if you are starting from 1.5 * 10^6, the formula becomes:
8.0 * 10^6 = 1.5 * 10^6 * e^(.3662040962 * t)
divide both sides of the equation by 1.5 * 10^6 to get:
8.0 * 10^6 / (1.5 * 10^6) = e^(.3662040962 * t)
take the natural log of both sides and simplify to get:
ln(5 + 1/3) = .3662040962 * t
solve for t to get:
t = ln(5 + 1/3) / .3662040962 = 4.571157043
to confirm, take 1.5 * 10^6 and multiply it by e^(.3662040962 * 4.571157043).
you will get 8.0 * 10^6, as you should.
if you had started from 4.5 * 10^6, the formula would have become:
8.0 * 10^6 = 4.5 * 10^6 * e^(.3662040962 * t)
in that case, you would have solved for t to get:
t = ln(8.0 * 10^6 / (4.5 * 10^6) / .3662040962, resulting in:
t = 1.571157043
add that to the 3 hours to get from 1.5 * 10^6 to 4.5 * 10^6 and the total hours is 4.571157043.
the total hours to get from 1.5 to 4.5 million = 3.
the total hours to get from 4.5 to 8 million = 1.571157043
the total hours to get from 1.5 to 8 million = 4.571157043
the formula for this problem can be graphed as shown below:
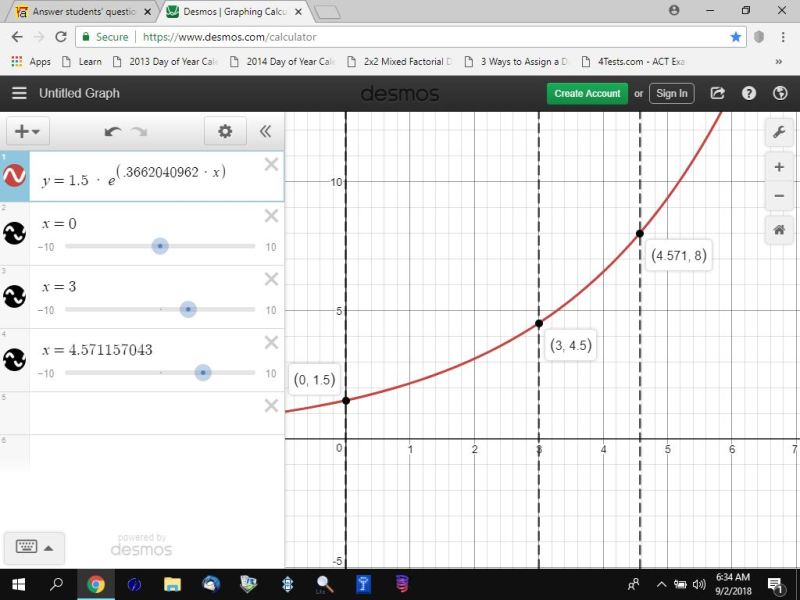
|
|
|