Question 1119676: Find the exact location of all the relative and absolute extrema of the function. (Order your answers from smallest to largest x.)
k(x) = 2x/3+ (x + 1)^(2/3) with domain (−∞, 0]
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!
k(x) =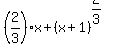 
k'(x) = 
(1) Set k'(x) = 0 to look for local extrema.
 [by cubing both sides of the equation]
The point (-2, -1/3) is a local extremum. To see if it is a local maximum or a local minimum, check the second derivative.
k''(x) =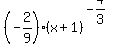 
k''(-2) = 
The second derivative is negative at x = -2, so (-2,-1/3) is a local maximum.
(2) Other local extrema can occur where the first derivative is undefined.
For this function, the derivative is undefined at x = -1. For x slightly less than -1 (more negative than -1), the derivative is large negative; for x slightly more than -1 (less negative than -1), the derivative is large positive.
Since the derivative changes suddenly at x = -1 from large negative to large positive, there is a local minimum at x = -1, as long as the function is defined there.
The function is defined at x = -1:
k(-1) = 
So the point (-1,-2/3) is a local minimum.
(3) For absolute extrema, we need to check the function values at the endpoints of the given domain.
Inspection shows that the derivative is always positive for x less than -2; that means as x goes to negative infinity there is no absolute minimum value.
For the absolute maximum value, inspection again shows that the derivative is always positive for x greater than -1. That means the absolute maximum is at the right endpoint of the domain.
So the absolute maximum is (0,k(0)) = (0,1).
|
|
|
