Question 1118869: A small airplane at an altitude of 5000 feet is flying East at 300 feet per second, and you are watching it with a small telescope as it passes directly overhead. Refer to the figure above.
a. What is the slope of the telescope 5, 10, and 20 seconds after the plane passes overhead?
b. What is the slope of the telescope t seconds after the plane passes overhead?
c. After it passes overhead, is the slope of the telescope increasing, decreasing, or staying the same?
The solution for the first requirement from question a is provided as follows:
at 5 sec.:
speed = 300 ft/sec
distance = speed * time
= (300 ft/sec)
= 1,500 ft
slope = vertical distance/horizontal distance
Round off your answers to two decimal places.
(Answer should be in this format:)
a. at 10 sec, slope = _____at 20 sec, slope = 0._____
b. slope at t seconds = _____/t
c. _____
Found 2 solutions by josgarithmetic, Theo:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5 seconds
300*5=1500 feet
10 seconds
300*10=3000 feet
20 seconds
300*20=6000 feet
-
t seconds after pass overhead
slope, 
Decreasing slope, after plane passes overhead
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the slope of the telescope in relation to the ground is equal to the vertical distance divided by the horizontal distance.
the vertical distance stays the same because the plane is flying at a constant altitude of 5000 feet.
the horizontal distance is changing because the plane is moving at 300 feet per second in a horizontal direction.
at 0 seconds, the slope is undefined because vertical distance divided by horizontal distance becomes 5000 / 0 which is undefined.
at 5 seconds, the vertical distance is 5000 and the horizontal distance is 300 * 5 = 1500.
the slope is therefore 5000 / 1500 = 3.33 rounded to 2 decimal places.
at 10 seconds, the vertical distance is 5000 and the horizontal distance is 300 * 10 = 3000.
the slope is therefore 5000 / 3000 = 1.67 rounded to 2 decimal places.
at 20 seconds, the vertical distance is 5000 and the horizontal distance is 300 * 20 = 6000.
the slope is therefore 5000 / 6000 = .83 rounded to 2 decimal places.
at T seconds, the vertical is 5000 and the horizontal distance is 300 * T.
the slope is therefore 5000 / (300 * T).
answers to your questions:
a. What is the slope of the telescope 5, 10, and 20 seconds after the plane passes overhead?
slope is 3.33 at 5 seconds.
slope is 1.67 at 10 seconds.
slope is .83 at 20 seconds.
b. What is the slope of the telescope T seconds after the plane passes overhead?
slope is 5000 / (300 * T) at T seconds.
c. After it passes overhead, is the slope of the telescope increasing, decreasing, or staying the same?
the slope is decreasing.
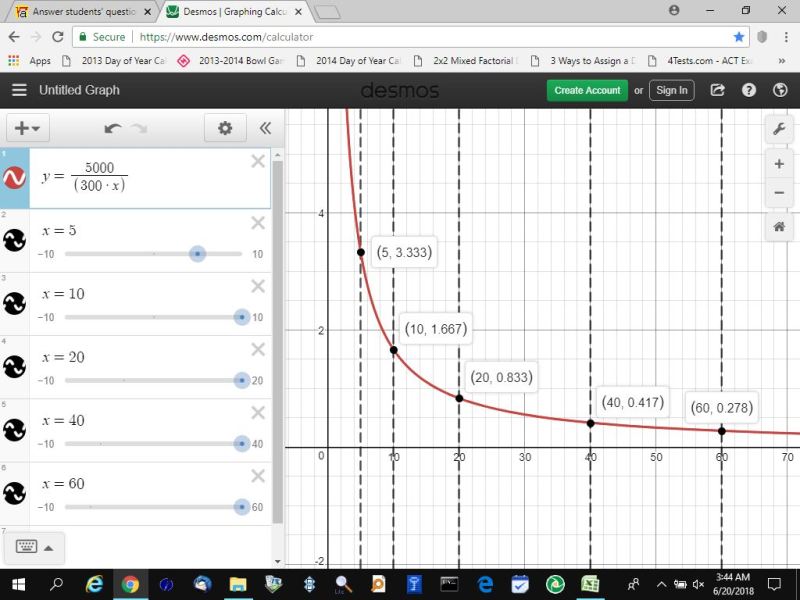
this can be seen in the following graph, where y represents the slope and x represents the number of elapsed seconds.
the coordinate points are in (x,y) format.
(5,3.333) means 5 seconds elapsed with a slope of 3.333.
the graphing software rounds to 3 decimal places.
you can see that the slope is decreasing as the number of elapsed seconds gets larger.
visually, it looks like this:
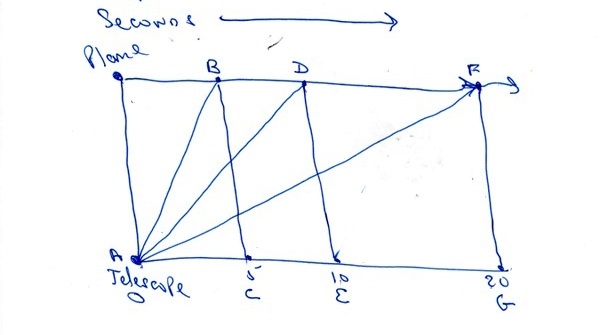
at 5 seconds, triangle ABC is formed.
the vertical leg is BC with a length of 5000 feet.
the horizontal leg is AC with a length of 300 * 5 = 1500 feet.
the slope is 5000 / 1500 = 3.33 rounded to 2 decimal places.
at 10 seconds, triangle ADE is formed.
the vertical leg is DE with a length of 5000 feet.
the horizontal leg is AE with a length of 300 * 10 = 3000 feet.
the slope is 5000 / 3000 = 1.67 rounded to 2 decimal places.
at 20 seconds, triangle AFG is formed.
the verttical leg is FG with a length of 5000 feet.
the horizontal leg is AG with a legnth of 20 * 300 = 6000 feet.
the slope is 5000 / 6000 = .83 rounded to 2 decimal places.
|
|
|