Question 1085090: This was a question on my cct part 2 and i did not understand it at all.
Find the length of the other two sides of a right angle triangle if the hypotenuse is 15cm and one side is 3cm longer than the other side.
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This was a question on my cct part 2 and i did not understand it at all.
Find the length of the other two sides of a right angle triangle if the hypotenuse is 15cm and one side is 3cm longer than the other side.

This triangle represents a 3-4-5 Pythag. triple, TIMES 3.
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the shorter leg of the triangle, in centimeters.
Then the length of the longer leg is (x+3) cm, according to the condition.
The Pythagorean theorem says
 = = 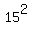 , or , or
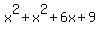 = 225, = 225,
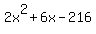 = 0, = 0,
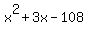 = 0.
Factor left side:
(x-9)*(x+12) = 0.
The roots are x= 9 and x= -12.
Ignore the negative root, since the length can not be negative.
The only solution to the problem is x= 9 cm.
Answer. The legs of the given right-angled triangle are 9 cm and 12 cm.
It is the classic (3-4-5)-right-angled triangle. = 0.
Factor left side:
(x-9)*(x+12) = 0.
The roots are x= 9 and x= -12.
Ignore the negative root, since the length can not be negative.
The only solution to the problem is x= 9 cm.
Answer. The legs of the given right-angled triangle are 9 cm and 12 cm.
It is the classic (3-4-5)-right-angled triangle.
To see more similar solved problems, look into the lesson
- Solved problems on the perimeter and side lengths of a triangle
- Solved problems on the perimeter and side lengths of a right-angled triangle
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Finding the perimeter and sides lengths of triangles, parallelograms, rectangles and polygons".
|
|
|