Question 1040859: Q: An increase in geometric progression has positive terms.The sum of the first eight terms is seventeen times the sum of the first four terms.The seven term is 960.The ninth term is?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In geometric progression, each term is equal to the one before times a certain number called the common ratio,  . .
If we call the first term  , ,
everything else can be calculated from  and and  . .
The  term is term is  , ,
and the sum of the first  terms is terms is
 . .
If we knew  and and  , ,
we could calculate
the sum of the first  terms as terms as
 ; ;
the sum of the first  terms as terms as
 ; ;
the 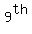 term as term as
 , and , and
the 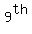 term as term as
 . .
The problem tells us that
"the sum of the first eight terms is seventeen times the sum of the first four terms" ,
so  or or  , and , and
"the seventh term is 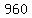 " , " ,
so  or or  . .
From the two equations above, we can find  and and  , ,
and from  and and  , ,
we can find  . .
Alternately,  . .








Then 
So,  . .
|
|
|